Understanding Radiometric Dating
Would you like to understand exactly how radiometric dating works? It’s really not very difficult. The following video summarizes the ideas, which are explained in a little more detail below.
Technical note: The video above and example below assume that potassium-40 decay always proceeds directly to argon-40. In reality, other decay pathways occur simultaneously, and real radiometric dating requires taking into account all of them. We’ve focused on only one keep the example simpler.
Elements and Isotopes
Recall that atoms are made from protons, neutrons, and electrons, with the protons and neutrons forming the central nucleus of the atom. Each different chemical element is characterized by the number of protons in its nucleus, which we call the element’s atomic number. For example, carbon has atomic number 6, meaning that carbon nuclei always have 6 protons, and oxygen has atomic number 8, meaning that oxygen nuclei always have 8 protons.
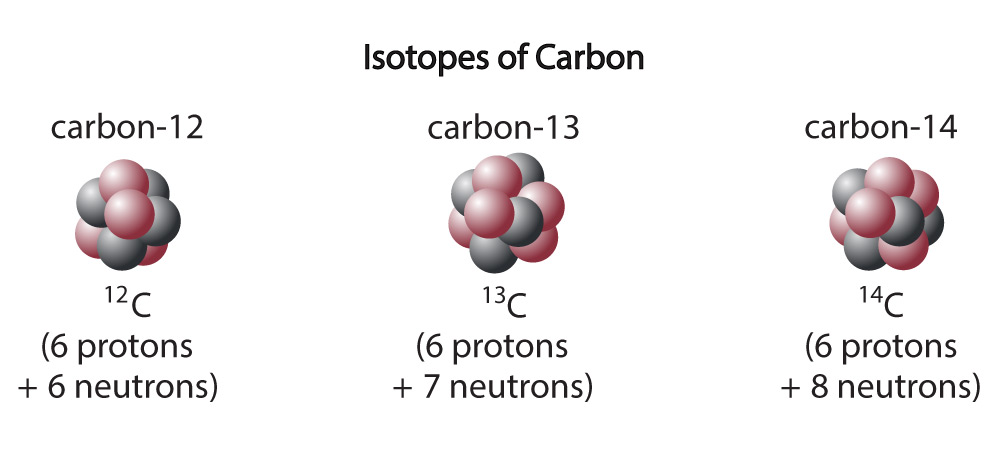
While a particular chemical element always has the same number of protons, it can come in different forms — called isotopes — that have different numbers of neutrons. For example, Figure 1 shows that carbon atoms come in three different isotopes (Figure 4.14): carbon-12, which has 6 neutrons in addition to the 6 protons; carbon-13, which has 7 neutrons; and carbon-14, which has 8 neutrons.
Stable and Radioactive Nuclei
Most of the atoms and isotopes we encounter in daily life are stable, meaning that their nuclei stay the same at all times. For example, most of the carbon in our bodies is carbon-12, which is stable (carbon-13 is also stable). But some isotopes are radioactive , meaning that their nuclei are prone to spontaneous change, or decay . Carbon-14 is an example of a radioactive isotope: it undergoes spontaneous decay in which one neutron becomes a proton, so that what was previously carbon-14 (6 protons and 8 neutrons) becomes nitrogen-14 (7 protons and 7 neutrons).
Note: the original radioactive isotope (the carbon-14 in this case) is often called the “parent isotope,” and the new atom it turns into after decay (the nitrogen-14 in this case) is often called either the “daughter isotope” or the “decay product.”
The Concept of Half-life
Radioactive decay always occurs at the same rate for any particular radioactive isotope, and scientists can measure these rates in the laboratory. We generally characterize the decay rate of an isotope by stating its half-life — the length of time it would take for half its nuclei to decay.
For example, the half-life of carbon-14 is about 5,700 years. This means that if a bone starts out with some particular amount of carbon-14, it will have only half that amount remaining after 5,700 years, one-quarter that amount remaining after 2 5,700 = 11,400 years, one-eighth that amount after 3 5,700 = 17,100 years, and so on. Therefore, by figuring out how much of the original carbon-14 remains, we can determine the age of the bone. This is the essence of radiometric dating.
Note that radiometric dating with carbon-14 (sometimes called “carbon dating” or “radiocarbon dating”) has a fairly obvious limitation: Because its half-life is “only” 5,700 years, by the time a bone gets to an age of more than about 60,000 years, there will be so little carbon-14 remaining that we can no longer determine its age.
Fortunately, many other radioactive materials have much longer half-lives. For example, uranium-238 has a half-life of about 4.5 billion years. Since that also happens to be the approximate age of the Earth and the solar system, this means that half of the uranium-238 atoms that existed when the solar system was born are still present in the solar system; the other half have turned into lead.
Note: You might wonder how scientists can measure such long half-lives. The answer is that because radioactive decay always proceeds at the same steady rate, you can calculate the half-life of any radioactive isotope based on observing its decay in the laboratory for a much shorter period of time, such as a few months to a few years.
A Radiometric Dating Example
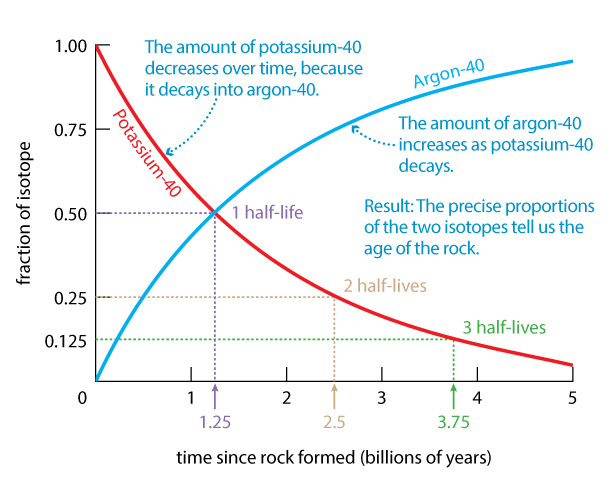
One of the most common isotopes used in radiometric dating is potassium-40, which decays into argon-40 with a half-life of 1.25 billion years. Potassium is a common element in many minerals, and there is always some radioactive potassium-40 mixed in with stable potassium. Argon-40 is a gas, which means it is never present in rocks when they first form (since gases would escape). Therefore, if we find argon-40 trapped inside a rock that also contains potassium-40, we know that the argon-40 must be a result of radioactive decay.
To see how this idea is useful, imagine a small piece of rock that contained 1 microgram of potassium-40 when it formed (solidified) long ago. The half-life of 1.25 billion years means that half the original potassium-40 would have decayed into argon-40 by the time the rock was 1.25 billion years old, so at that time the rock would contain ½ microgram of potassium-40 and ½ microgram of argon-40. Half of this remaining potassium-40 would then have decayed by the end of the next 1.25 billion years, so after 2.5 billion years the rock would contain ¼ microgram of potassium-40 and ¾ microgram of argon-40. After three half-lives, or 3.75 billion years, only 1/8 microgram of potassium-40 would remain, while 7/8 microgram would have become argon-40. Figure 2 summarizes the gradual decrease in the amount of potassium-40 and corresponding rise in the amount of argon-40.
You can therefore use the graph in Figure 2 to figure out the age of a rock. For example, suppose you find a rock that contains 3 times as much argon-40 as potassium-40. As the graph and the above discussion show, this means that ¾ of the original potassium-40 has by now decayed into argon-40, which means the rock is 2.5 billion years old.