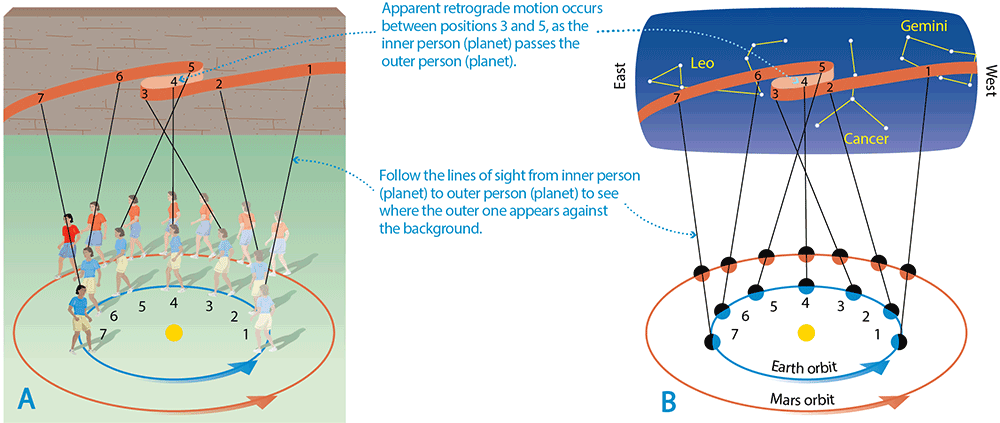
Take a moment to briefly review planetary motion in our sky, as we discussed in Section 2.4. Recall that over many weeks or months, planets can undergo what we call apparent retrograde motion, and that the reason for this motion is very simple: it occurs as we pass by a planet (or the planet passes by us) in our orbit around the Sun.
As we discussed at the end of Chapter 2, this leads to an interesting question: Given that the ancient Greeks had already recognized that our world is round, why didn’t they take the next step and use their observations of planetary motion to also recognize that we orbit the Sun?
In fact, they did consider this possibility; of particular note, a Greek astronomer and mathematician named Aristarchus of Samos (c. 310–230 B.C.) argued that Earth must orbit the Sun, which means he correctly realized that the Sun, not Earth, is the center of our solar system. However, he did not succeed in convincing most other scholars of the time. One reason that most other scholars rejected the correct answer was that we don’t feel Earth’s motion as it rotates and orbits. But another reason why many scholars rejected the correct idea had to do with something called parallax .
Parallax in Everyday Life
You may not have realized it, but you are very familiar with the idea of parallax, because it is something we see all the time. In fact, it helps us judge the relative distances of objects around us, which means it is important to everyday tasks such as being able to pick up a glass of water or catch a ball. To understand the idea, start by doing the following activity.
Activity
Part 1 – Parallax in Everyday Life
1. Extend your arm and hold up your index finger. Keeping your arm and finger still, look at your finger as you alternately open and close your left and right eyes. You should see something like what is shown in the video clip below. Can you explain why your finger appears to move, even though you are holding it still? (Note: if you have difficulty closing one eye at a time, have a friend instead cover your eyes one at a time with their hand or a piece of paper.)
Video
Everyday Parallax
2. Repeat the experiment while bending your arm so that your finger is closer to your face. You can try it with your finger at different distances. Then decide how you would complete this sentence:
Explain why this is the case.
3. Go outside and find a flagpole (or other pole). Take 3 steps back from the pole and look at it against the background in the distance. Then take one step to the left and look at it again (see figure below). Notice how the pole appears to shift against the background as you step to the left. If you keep stepping back and forth, you’ll see the pole seem to keep shifting back and forth, even though the pole is not moving. How is this similar to what you did with your extended finger? Explain why you see this parallax of the pole.

4. Move another 3 steps away from the pole and repeat your experiment. Is the parallax of the pole bigger or smaller than it was when you were closer? Explain why.
5. Repeat the experiment several more times, each time moving farther from the pole. Describe how its parallax changes as you move farther away from it. Can you move far enough away so that you can no longer notice the parallax?
6. Discuss how parallax helps us judge distances of objects around us, and how it can help us reach to pick up a glass of water or to catch a ball.
This first part of the parallax activity is to make sure students understand the basic idea of parallax as an apparent shift in an object’s position, and to realize that the amount of parallax gets smaller as the object gets farther away.
- For (1): This should be easy for students to see. For the explanation, try to get students to recognize that they are looking at their finger from a different position (angle) from their left and right eyes.
- For (2): The answer is that parallax gets smaller with distance (to their finger), and they should be able to see this.
- For (3): We’ve suggested taking only 3 steps away from the flagpole so that the parallax shift should be quite obvious as they step one step to the left. They can keep moving back and forth between their original position and the one step left to see the parallax clearly. Again, help them understand that the parallax is observed because of the changing position from which they are viewing the pole as they move back and forth.
- For (4) and (5): They should notice that the pole’s apparent shift, or parallax, gets smaller as they move farther away from it. It should be clear that if they were far enough away, they would no longer be able to notice the parallax.
- (6): Parallax is in essence the method by which we judge depth perception: we use our two eyes to judge distances because more distant objects have smaller parallax. And it is depth perception that makes it possible to reach for objects, catch balls, and so on.
Stellar Parallax
As you’ve seen, we should notice parallax for relatively nearby objects whenever our viewing position changes. This brings us to the key point: If Earth is orbiting the Sun, then our viewing position is always changing as we look to the stars. Let’s continue the activity to see how this works, and you’ll then be able to understand how it accidentally led the ancient Greeks to an incorrect conclusion.
Activity
Part 2 – Stellar Parallax
Continuing near the flagpole outside, bring a ball to represent the Sun and place it at least 10 steps away from the flagpole. Then do the following:
-
- Stand over the ball (“Sun”) without moving as you look toward the flagpole. Do you see any parallax of the flagpole while you stand still? Why or why not?

-
- Move about 2 steps away from the ball and start walking in a small “orbit” around it as you watch the flagpole (see figure). Do you see parallax of the flagpole? Why or why not?

-
- Continue walking your “orbit” and look at a variety of objects at different distances beyond the flagpole (such as other poles or trees). How does the amount of parallax you see depend on the distance of the object you are looking at? Why?
-
- Discuss: Note that in step (1), you observed no parallax when you stood still in the center of the “orbit.” Is there any circumstance in which you could be walking around your “orbit” but still see no parallax for an object beyond the flagpole? How?
- Discuss: Use what you’ve learned to explain why the fact that Earth orbits the Sun means we should see parallax as we look to the stars. Then explain how it might be possible for Earth to be orbiting the Sun but for the parallax of stars to be undetectable.
This second part of the parallax activity shows how this idea extends to stellar parallax. It will work best if you can set up the “orbit” around the ball at a location where students can see a variety of objects at various distances beyond the flagpole (for example, looking toward a playground or an area where you can see different trees at different distances).
• For (1): There is no parallax when you are standing still, because you are always looking from the same position.
• (2) You will now see parallax with the pole appearing to shift against the background as you view it from the different positions of the orbit.
• (3) The more distant objects will show smaller parallax, just as students found as the general rule for parallax in part 1 of the activity. Note: If there are no good objects to observe in the distance, you could have other students stand at different distances in a line behind the flagpole, and the “orbiting” student could look at the amount of parallax observed for the classmates at different distances.
• (4) If the object is far enough away, then you won’t be able to notice its parallax.
• (5) As discussed below the activity, parallax of nearby stars relative to more distant ones MUST occur if Earth orbit the Sun, but if the “nearby” stars are far enough away, then this parallax might be too small for us to detect.
Figure 3.3 shows that just as you saw parallax for the flagpole in the above activity, we should see parallax of stars as Earth orbits the Sun.
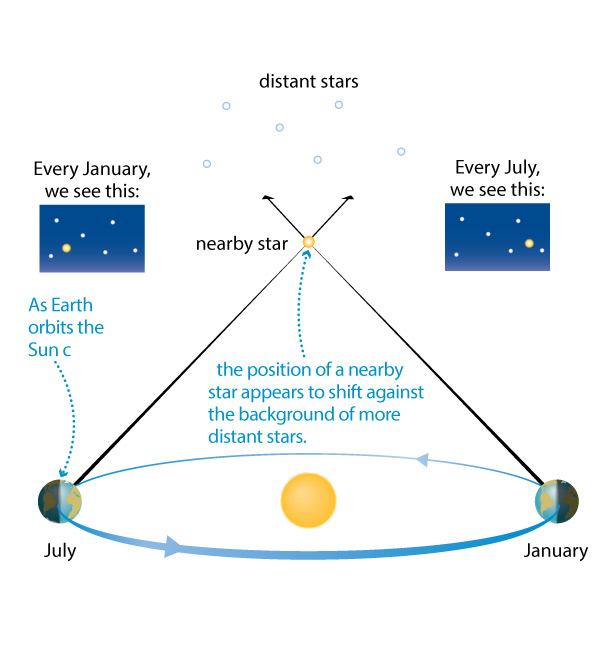
The ancient Greeks understood this idea; that is, they knew that if Earth orbited the Sun, then stellar parallax must exist. (Note: There is a slight subtlety here: Because the Greeks believed that all stars lie on the same celestial sphere, they expected to see stellar parallax in a slightly different way. If Earth orbited the Sun, they reasoned, at different times of year we would be closer to different parts of the celestial sphere and would notice changes in the angular separation of stars.)
How the Greeks Drew the Wrong Conclusion
So here was the problem: No matter how hard they searched, the ancient Greeks were unable to detect any stellar parallax at all. Before you read on, think about what this might mean by discussing the following.
Claim-Evidence-Reasoning Activity
Stellar Parallax
Imagine that while doing the stellar parallax activity (above), you also took a series of photos of an object in the distance during Step 1 when you were standing over the ball and again during the subsequent steps in which you were walking the small “orbit” around the ball. Now, imagine that the photos are shuffled and you are looking at two randomly selected photos from your set, and both photos show the distant object appearing to be in exactly the same place relative to the horizon; that is, the photos do not reveal any evidence of parallax for the object. In small groups use the Claim, Evidence, Reasoning format to evaluate the following claim:
Claim: There are two possible explanations for the lack of parallax: (1) Both photos were taken when you were not moving; that is, while you were standing over the ball in Step 1. (2) The photos were in fact taken while you were in different positions in the “orbit” around the ball, but the object was far enough away that its parallax was too small to be noticeable in the photos.
The goal of this CER activity is to get students to understand the logic behind the idea that, in general, there are two possible explanations for a lack of detectable parallax. For evidence, students should cite what they’ve learned from the activity for each of the two possibilities cited in the claim. For reasoning, they should be able to explain why no other possibilities are warranted.
The same type of reasoning led the ancient Greeks to realize that the lack of observable stellar parallax could mean only one of two things:
- Earth orbits the Sun, but the stars are so far away that stellar parallax is undetectable to the naked eye.
- There is no stellar parallax because Earth remains stationary at the center of the universe.
The correct answer, of course, is the first one: As you learned in Chapter 1, stars are really far away. In fact, the distance to even the nearest stars (the alpha Centauri system) is more than 100,000 times the distance across Earth’s orbit. In other words, if Figure 3.3 were drawn to scale, you’d have to put the “nearby star” more than 100,000 times as far away as shown in that figure. The parallax shift would then be so small that you’d have no chance of noticing it by naked eye, and there were no telescopes in ancient times.
Unfortunately, the Greeks could only guess how far away the stars might be, and with few exceptions (such as Aristarchus), they generally assumed that the stars could not possibly be so far away as to make parallax undetectable to our eyes. As a result, they rejected the correct answer, and instead concluded that the lack of detectable parallax must mean that Earth is located at the center of the universe. In a sense, you might say that the Greeks reached the conclusion that Earth lies at the center of the universe because they suffered from “a failure of imagination” about how big the universe might actually be.
Today, astronomers can detect stellar parallax with the aid of telescopes, providing direct proof that Earth really does orbit the Sun. Careful measurements of stellar parallax also provide the most reliable means of measuring distances to nearby stars.
Key Concepts: Proof that Earth Orbits the Sun
The fact that we can observe stellar parallax with telescopes provides direct proof that Earth really does orbit the Sun. There is no other possible explanation for the observed parallax of the stars.
The Greek Explanation for Apparent Retrograde Motion
Think once more about the apparent retrograde motion of the planets that we see in the sky. As we’ve discussed, this motion has a simple explanation in a Sun-centered solar system (see: Figure 2.34.)
However, if you believed that Earth is the center of the universe, as did most of the ancient Greeks, then it would be much more difficult to explain, because the observed retrograde motion would imply that the planets actually do sometimes turn around and go backward in their orbits around Earth. How could planets that supposedly reside on “celestial spheres” like those shown in Figure 3.1 ever go backward?
In fact, the question of apparent retrograde motion was even more challenging for the ancient Greeks, because they also believed in an idea sometimes called “heavenly perfection,” and they interpreted “perfection” to mean that all motions in the heavens must be in perfect circles. In other words, the Greeks needed to find a way to explain apparent retrograde motion while having the planets always move only in perfect circles around the Earth. You might think about this for a moment, and see if you can come up with a way that this could in principle occur.
Did you come up with any ideas? Most people don’t, but the Greeks spent centuries working on this problem, and they ultimately succeeded in coming up with what was, at least at the time, a viable model. Figure 3.4 (and the associated video) shows how it worked.
Figure 3.4 – This diagram shows how Ptolemy’s Earth-centered model accounted for apparent retrograde motion. Each planet is assumed to move around a small circle that turns upon a larger circle. The resulting path (dashed) includes a loop in which the planet goes backward as seen from Earth. Credit: The Cosmic Perspective
Even with this idea of circles upon circles, the Greeks found that it was still difficult to use this model to explain their observations of planets in the sky. Nevertheless, they kept trying, gradually adding more and more features (such as additional small circles and shifting some of the circles off-center) to the model. In its final form, published by the Greek astronomer Ptolemy (pronounced “tol-e-mee”) in about 150 A.D., the model was very complex but mathematically detailed enough that it could be used to predict where planets would appear in the sky on any particular date.
The necessary calculations were difficult and tedious, but they ended up working reasonably well: In general, the predictions were correct to within a few degrees, which is smaller than the angular size of your fist held at arm’s length (see Figure 2.8).
It was this seeming success — a model that gave “pretty good” predictions of planetary positions — that kept the Earth-centered idea in use for almost 1,500 years after Ptolemy’s death. Indeed, when Ptolemy’s book describing the model was translated by Arabic scholars around A.D. 800, they gave it the title Almagest, derived from words meaning “the greatest work.” Of course, not everyone was so enamored of the model, particularly those who tried to do its tedious calculations. For example, during the 13th century, the Spanish monarch Alphonso X (1221–1284) commissioned a new set of calculations of planetary positions based on Ptolemy’s model. Commenting on the tedious nature of the work, the monarch is said to have complained, “If I had been present at the creation, I would have recommended a simpler design for the universe.”
Discussion
Should a Model Reflect Reality?
Today, we usually think that scientific models should be at least reasonable approximations of reality. But the ancient Greeks did not necessarily hold this view. For example, Ptolemy’s model was so complex (much more so than we’ve discussed here) that even Ptolemy himself seems not to have thought that planets really moved in the way his model suggested. Instead, he (and others) probably thought of the model simply as a useful tool for calculating where planets would appear in the sky, he may not have even cared about how planetary orbits really work. Do you think that models should reflect reality? Are there circumstances in which models can be useful even if they are wrong? Defend your opinions.
This optional discussion delves into the nature of models. There is no right or wrong answer, but it should spur interesting discussion. For example, as noted, we generally expect modern scientific models to reflect reality. Nevertheless, we still often make use of models that we know are “wrong,” such as using the celestial sphere model to describe the positions of stars and constellations in our sky. Another example which your students may have learned in the past is the model of the atom in which we imagine electrons “orbiting” the nucleus, which can give useful results, but which is also known to be incorrect according to quantum physics.
Take It To The Next Level
“Triangulation”: Using Parallax to Measure Distance”Triangulation”: Using Parallax to Measure Distance