“No Greenhouse” Temperatures
The mathematics needed to predict a world’s temperature with the greenhouse effect is fairly complex. However, it is quite easy to calculate the temperature we would expect if there were no greenhouse effect. In that case, the average surface temperature of any world in our solar system would depend on only two major factors:
- The world’s distance from the Sun, which determines how much sunlight reaches the world.
- The relative proportions of this sunlight that the world’s surface absorbs and reflects (because only the absorbed sunlight heats the surface). We usually describe this simply by stating the world’s reflectivity , which is the fraction of the arriving sunlight that is reflected by the world’s surface and/or clouds.
The following formula can be used to calculate the temperature (in Celsius) that a world in our solar system would have based on these two factors. We call this temperature the “no greenhouse” temperature, because it is the temperature the world would have if there were no greenhouse effect.
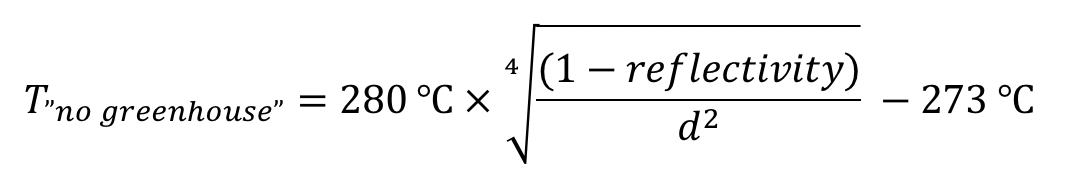
where d is measured in astronomical units (AU)
The 4√ symbol means the fourth root, or 1/4 power. You can find the fourth root on a calculator by raising to the ¼ power.
Example: Earth’s reflectivity is about 0.29, meaning that it reflects about 29% of the sunlight that reaches it. What is Earth’s “no greenhouse” temperature, and what would it be if Earth were instead located at Venus’s distance from the Sun (which is 0.723 AU)?
Solution
Step 1 Understand the problem. We can use the “no greenhouse” formula above to answer both questions. In both cases, we’ll set reflectivity = 0.29. For the first case, we use Earth’s actual distance from the Sun of d = 1 AU. For the second case, we’ll use Venus’s distance from the Sun of d = 0.723 AU.
Step 2 Solve the problem. We simply plug in the values for the two cases:
Case 1: Earth’s real distance of 1 AU:

Notice that this is well below freezing, since freezing on the Celsius scale is 0°C.
Case 2: If Earth were at Venus’s distance of 0.723 AU:

Step 3 Explain your result. If you think about the results of the calculations, you’ll notice two really interesting facts. First, without a greenhouse effect, Earth’s average temperature would be about −16°C (3°F), which is well below freezing. This tells us that the greenhouse effect must be very important to life on Earth, because without it our planet would be frozen over. Second, we’ve found that, by itself, putting Earth at Venus’s closer distance to the Sun would raise the temperature only to about 29°C (84°F), which is far below Venus’s actual temperature of 470°C (880°F). This confirms that distance from the Sun alone cannot explain Venus’s high temperature.
Check Your Skills
Venus’s reflectivity is considerably higher than Earth’s, because it is completely covered by clouds that reflect a lot of sunlight. In fact, measurements show that Venus’s reflectivity is about 0.75, meaning that it reflects about 75% of the sunlight that reaches it. Calculate Venus’s “no greenhouse” temperature using its actual reflectivity, and explain the meaning of your result.
First, for both the example in the box and the “Check your skills” question, be sure to note that the fourth root term may be difficult for some students, so you may need to help students learn how to do this calculation on a calculator. Once they understand how to do that, the solution to the “Check your skills” is identical to Case 2 above, except instead of using Earth’s reflectivity of 0.29 you use Venus’s reflectivity of 0.75. The result is:
Venus:
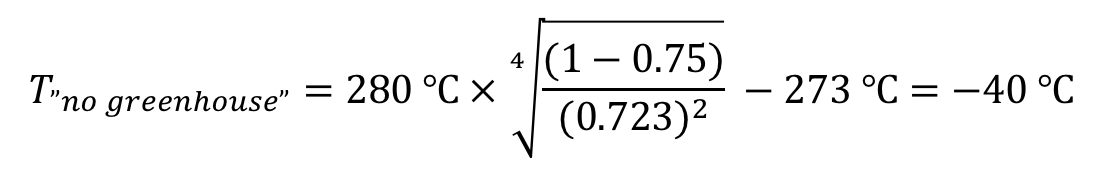
Note that this is even colder than Earth’s “no greenhouse” temperature of –16°C. In other words, Venus’s reflectivity is so high that, in the absence of a greenhouse effect, Venus would be colder than Earth, despite being closer to the Sun.
Notes on the formula: We gave the formula in this box without derivation, because the full derivation is beyond the scope of this book. However, if you or your students are curious about its form, the basic ideas are fairly easy to understand:
- The term (1 − reflectivity) is the proportion of sunlight that a world absorbs, which is the light that heats its surface.
- This term is divided by d2 because the amount of energy from sunlight (per unit area) declines with the square of distance from the Sun (that is, like gravity, it follows an inverse square law).
- The full term (1 − reflectivity)/d2 therefore represents the total amount of energy that the world absorbs from sunlight (per unit area) each second.
- This energy warms the surface, and the surface returns the energy to space by emitting what we call thermal radiation, which is radiation that depends only on an object’s temperature (it is sometimes also called “blackbody radiation”). The amount of thermal radiation emitted from any object (per unit area) depends on temperature raised to the fourth power (this is embodied in what is often called the “Stefan-Boltzmann law”); that is why calculating the world’s temperature requires taking the fourth root of the absorbed energy.
- The 280°C in the formula is simply a constant based on the luminosity of our Sun. This constant would be different if we were considering worlds orbiting a different star.