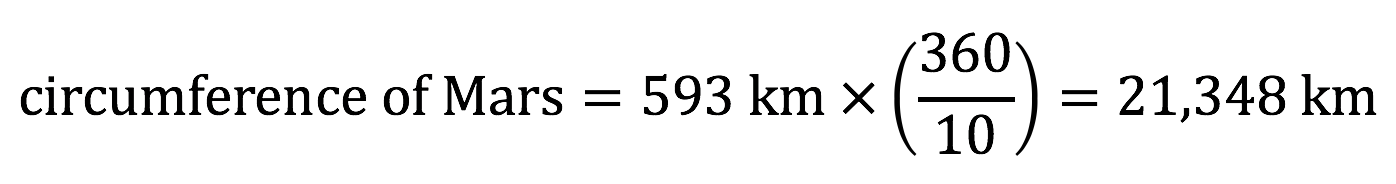Do The Math
Measuring Earth’s Circumference.
The first known measurement of Earth’s size was made by the Greek scientist Eratosthenes (pronounced Erah-TOSS-then-ese) in about 240 b.c. He successfully calculated Earth’s circumference by comparing the noon altitude of the Sun on the same day in two locations and applying a little geometry.
While studying in Alexandria, Eratosthenes learned of accounts that described how, at noon on the summer solstice, structures in a city to the south called Syene (modern-day Aswan) cast no shadows, indicating that the Sun was passing directly overhead (at the zenith). This caught Eratosthenes attention, because he observed something different in Alexandria: The noon shadows on the summer solstice indicated that the Sun was passing 7° away from directly overhead. Figure 1 shows how the noon shadows differed in the two cities.


The Greeks already knew that Earth was round (spherical), so with a little geometry, Eratosthenes recognized that Alexandria had to be 7° of latitude north of Syene. As Figure 2 shows, the fact that 7° is 7/360 of a circle means that the north-south distance between the two cities must be 7/360 of the circumference of Earth.
Eratosthenes estimated the north-south distance between Syene and Alexandria to be 5000 stadia (the stadium was a Greek unit of distance). He thereby concluded that:

If you multiply both sides by 360/7 , you’ll find that this equation implies that Earth’s circumference is about 260,000 stadia.
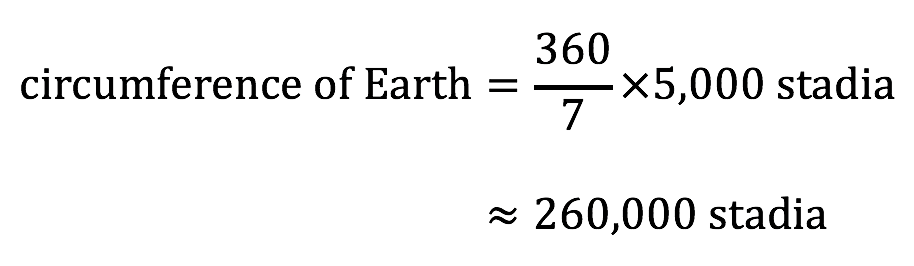
Based on the actual sizes of Greek stadiums, historians estimate that stadia must have been about 1/6 km each, making Eratosthenes’s estimate about
(260,000/6) ≈ 43,000 kilometers—impressively close to the real value of just over 40,000 kilometers.
Check Your Math Skills: Use Eratosthenes’ Method to Calculate the Circumference of Mars
Imagine you are part of the first exploratory team to land on Mars. You and your team measure the Sun’s noon-time altitude in the sky. Over the next few days your team drives a pressurized rover due south, covering a total distance of 593 km. At your stopping point you measure the noontime inclination of the Sun again, and this time you find it to be 10° closer to the zenith than it was at your starting point. Use the given data and the method of Eratosthenes to calculate the circumference of Mars.
Students should be able to follow the example to set up a similar equation, showing that the two different measured angular positions of the sun imply that the distance covered in the rover covers 10/360 of the circumference of Mars: