We are now ready to discuss the last three items on our list from the beginning of this section of six key things that gravity does:
Gravity keeps satellites, the International Space Station, and the Moon in orbit of Earth
Gravity keeps Earth and other planets in orbit around the Sun.
Gravity holds galaxies together.
All three of these relate to orbits, which means you already know how to explain them. Recall that once Newton came up with the universal law of gravitation, he was able to use mathematics to show that it predicted what Kepler had already discovered: that it leads less massive objects (like planets) to orbit more massive ones (like the Sun), and that the force holding the planets in orbit gets weaker with distance, thereby explaining Kepler’s discovery that more distant planets orbit the Sun at slower speeds.
In fact, Newton found that the universal law of gravitation applies in the same way to all orbiting objects. Applying this idea to the three things from the list above:
- Because Earth is much more massive than satellites, the International Space Station, or the Moon, Earth’s gravity can hold these objects in orbit.
- The Sun holds Earth and other planets in orbit because the Sun is so much more massive than any of the planets.
- Galaxies are made up of stars, so all of a galaxy’s stars together contribute to the overall gravity of the galaxy. This gravity is what keeps the stars all orbiting around the center of the galaxy. (Note: In addition to the gravity of stars, galaxies also have gravity from gas that they contain and from the mysterious “dark matter” that seems to make up the majority of the mass in most galaxies.)
Discussion
Gravitationally Bound
Use what you know about gravity weakening with distance to explain the following. Hint: The key to answering the second and third questions lies in remembering that there are many stars in a galaxy and many galaxies in the universe.
- Jupiter has many moons that orbit it, but beyond a certain distance, it has no more moons.
- If a “planet” were too far from the Sun, it would not be able to orbit the Sun.
- If a star were too far from the center of a galaxy, it would not be able to orbit the galaxy.
(1) Jupiter’s gravity weakens with distance. Close to it, Jupiter can hold moons in orbit. But beyond a certain distance (about 200 Jupiter diameters), a moon would drift away from Jupiter due to gravitational perturbations from other planets, and therefore would escape and become an object orbiting the Sun independently.
(2) As the hint notes, the key to answering this question is to think about the fact that there are many other stars in our galaxy. The Sun’s gravity weakens with distance, so at some point, a “planet” would feel a weaker gravitational pull from the Sun than it would from other stars, which means it would no longer be held in orbit of the Sun.
(3) The same basic idea applies as for (2), except here it is the attraction that a star will eventually feel from other galaxies, once it gets far enough away from the center of its own galaxy.
Activity
What if the Sun Disappeared?
Pair up with a partner. One of you will represent the Sun, while the other will be the Earth in orbit around the Sun. Complete a few “orbits” around the Sun-partner.
Now imagine that the Sun disappears, instantaneously. Freeze your position in your orbit and have the partner representing the Sun step aside. Discuss with your partner: How would Earth’s motion be affected? What about other planets?
Challenge question: Hold a similar discussion to consider what would happen to the International Space Station if the Earth suddenly disappeared. What would happen to the International Space Station?
The key to answering the questions is to recall Newton’s first law of motion, which tells us that in the absence of a force, an object will move at constant velocity, meaning constant speed in a straight line. However, there are also a few subtleties that you may wish to discuss with students.
- For the first question: The Sun provides the gravitational force holds Earth and other planets in orbit. Therefore, if the Sun were removed, each planet would fly off in a straight line from whatever point it was at in its orbit when the Sun disappeared. A subtlety to keep in mind is that our entire solar system is orbiting the center of the Milky Way Galaxy, and the disappearance of the Sun would have a negligible effect on the galaxy’s total mass. Therefore, while the planets would fly off in what looks like straight lines after the Sun disappeared, they would in fact still be orbiting the galactic center.
- For the challenge question: As a first level approximation, the effect of Earth’s disappearance on the ISS would be similar to that of the disappearance of the Sun on Earth: ISS would fly off in a straight line. However, there are additional subtleties here:
- Much like the planets continuing to orbit the galactic center in the first question, the ISS would continue to orbit the Sun in this case.
- But in this case, the orbital speed of ISS (28,000 km/hr) is a significant fraction of Earth’s orbital speed around the Sun (average 107,000 km/hr). Depending on the position of the ISS in orbit at the time of Earth’s disappearance, the speed of the ISS in its new solar orbit could therefore be anywhere between 107,000 – 28,000 = 79,000 km/hr and 107,000 + 28,000 = 135,000 km/hr.
- The precise orbit of the ISS around the Sun will depend on both its initial direction at the time of Earth’s disappearance and its orbital velocity.
- The Moon’s gravity will also have a small effect on the final orbit around the Sun, though of course the Moon will also fly off with Earth’s disappearance.
Masses of Distant Objects
Have you ever wondered how scientists can know the masses of distant objects, such as of the Moon, or of the Sun, or of an entire galaxy? Or how we know the mass of our own planet? The answer is that the universal law of gravitation makes it possible to calculate masses in any case in which we can observe one object orbiting another.
To understand how this is possible, recall that Kepler discovered that planets farther from the Sun orbit more slowly than those closer to the Sun, and that this fact implies that it is a force from the Sun that holds the planets in orbit. Newton discovered this force to be gravity and his universal law of gravitation (in equation form) allows us to calculate the gravitational force that explains these orbits. Because the gravitational force depends on the Sun’s mass, it is possible to “work backward” from the orbital properties of any planet — more specifically, the planet’s average orbital distance and orbital period — to determine the mass of the Sun.
Note that because this idea works for any planet (you’ll get the same answer for the Sun’s mass no matter which planet you use), we can even use Earth’s orbital properties. In other words: Simply by knowing Earth’s orbital distance (about 150 million kilometers) and orbital period (one year), it is possible to calculate the mass of the Sun.
The same idea applies to all other cases in which one object orbits another. For example:
- Scientists can calculate Earth’s mass from the orbital period and distance of our Moon or of any artificial satellite.
- Scientists can calculate the mass of the Moon from the orbital period and distance of a spacecraft sent to orbit around it.
- Scientists can calculate the mass of Saturn from the orbital period and distance of any of its moons.
- Scientists can calculate the mass of a distant galaxy by measuring the orbital properties of stars or gas clouds orbiting its center.
- If a distant star is a member of a binary star system, scientists can calculate its mass by measuring the orbital properties of its companion star.
In fact, everything we know about masses of objects throughout the universe ultimately traces back to calculations based on the universal law of gravitation and observations of orbital properties.
Quick Quiz
Note: As always, after you finish the quiz, be sure you read the feedback that explains the correct answers, to make sure you understand the reasons for these answers.
The following box shows how you can calculate masses for yourself with the equation known as “Newton’s version of Kepler’s Third Law.” It gets this name because Kepler’s third law describes how orbital periods and distances are related, and Newton then used his universal law of gravitation to generalize this law into a form that also allows the determination of masses.
Take It To The Next Level
Calculating Masses with Newton’s Version of Kepler’s Third Law
(Coming Soon)
No Need for Fuel
Earth has been orbiting the Sun since the solar system was born some 4 ½ billion years ago. Have you ever thought about how it keeps going year after year?
The answer is that because there is no friction or air resistance in space, there is nothing to slow Earth down. As a result, it follows a path determined only by gravity, and the Sun’s gravity dominates the solar system. Therefore, Earth orbits the Sun on essentially the same path year after year. (The only deviations from being exactly the same path arise from the very small gravitational tugs on Earth caused by the Moon and by other planets.)
The same idea applies to other objects in space. As long as there is no friction, they will remain on orbital paths determined only by gravity. That is why, after a spacecraft is launched, it no longer needs any fuel to keep going. The only exception is for spacecraft in low Earth orbit, where there is still a tiny bit of friction from Earth’s upper atmosphere. These spacecraft can be slowed by this friction, causing their orbits to decay until they ultimately plummet back into the atmosphere (where they generally burn up, because they are coming in at such high speed).
Discussion
Free-Flying Astronaut
Look back at the photo that opened this chapter, showing an astronaut floating freely outside of his spacecraft. Note that both his spaceship (the Space Shuttle) and the astronaut were orbiting Earth at an orbital speed of about 28,000 km/hr. Can you explain why he didn’t fall behind the spacecraft when he was outside it?
This discussion applies the above ideas. Both the Shuttle and the astronaut were in orbit. Because they were already orbiting, and were in space where there was essentially no friction, their orbits were determined only by gravity. Initially, the astronaut was inside the Shuttle, and therefore was on exactly the same orbit as the Shuttle, with the same speed. Therefore, when he stepped out, he was still on the same orbit, traveling at the same speed. He could maneuver toward or away from the Shuttle by firing what were essentially tiny rocket engines on his spacesuit, but aside from those deliberate maneuvers (which were at very low speeds compared to the orbital speed), he would automatically remain with the Shuttle because they were both on the same orbit. This is similar to tossing a ball while riding in an enclosed car or a train. Since the ball has the same velocity as the vehicle, it will not “fall behind” when being tossed inside the moving vehicle.
Using Gravity to Steer Spacecraft
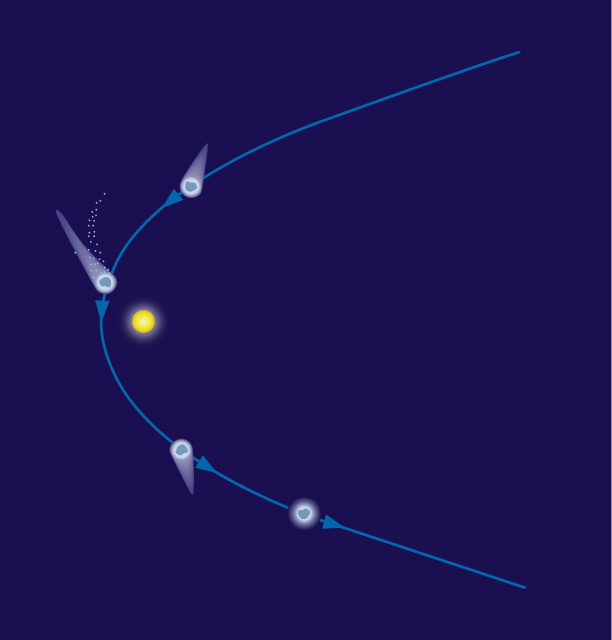
When you hear the term “orbit,” you probably think of one object going around another over and over again, just as Earth orbits the Sun year after year. However, gravity also allows objects to follow other paths. For example, some comets that come speeding into the inner solar system from afar simply curve around the Sun and then head back outward, never to return (Figure 3.34).
Scientists and engineers can use this same idea to “steer” spacecraft with gravity. Consider the New Horizons spacecraft, which flew past Pluto in 2015. Like any interplanetary spacecraft, New Horizons had to be launched from Earth with enough speed (called “escape velocity”) to allow it to escape the grip of Earth’s gravity and journey out into the solar system.
After that, however, New Horizons needed only very small amounts of fuel to make small course corrections, while all the rest of the “steering” was done by gravity. Engineers calculated exactly how the gravity of the Sun and planets would affect the spacecraft, and then chose a path that would make sure it reached Pluto. Figure 3.35 shows the path along with one of the spectacular photos of Pluto that the spacecraft took as it flew past.

Challenge Discussion
New Horizons Path
Watch the video animation of New Horizons path in Figure 3.35a, then discuss the following questions.
- How was the path of New Horizons past Jupiter similar to the path of the unbound comet shown in Figure 3.34?
- Notice that New Horizons actually gained a bit of speed as it passed Jupiter. How do you think it did this? Note that it did not involve firing any rocket engines.
- Notice that New Horizons flew right past Pluto a high speed. What would it have taken for New Horizons to slow down when it reached Pluto?
This is a somewhat challenging discussion, but could be fun for students. Answers:
1. The path past Jupiter is an unbound orbit, just like the unbound comet orbit in Figure 3.34. Scientists had deliberately aimed New Horizons toward Jupiter in order to be able to fly past it on this precise orbit.
2. This speed-increasing trajectory is what is sometimes called a “gravitational slingshot.” To understand it, notice that the spacecraft approached Jupiter in the same direction that Jupiter was orbiting the Sun. Therefore, as Jupiter’s gravity pulled the spacecraft toward it, Jupiter’s speed around the Sun was also adding to the spacecraft’s speed. Because the spacecraft was on an unbound orbit, it kept some of this speed as it left Jupiter behind.
3. The spacecraft approached Pluto on a high-speed, unbound orbit. Therefore, changing this orbit to a slower one would have required firing engines, which would have required a lot of fuel. That would have made the original spacecraft much heavier (for the weight of the fuel and the engines to fire), which would have made it much more expensive to build and launch.
Wow Factor!
Arrokoth
Take It To The Next Level
Orbital Mechanics (Coming Soon)
Orbiting Disks
As we’ve discussed, gravity’s central pull explains why virtually every large individual object in the universe — including stars, planets, dwarf planets, and large moons — is round.
There is also a second very common shape in the universe, though it applies only to collections of orbiting objects: this shape is a flattened disk. Examples include (Slide Show Figure 3.36):
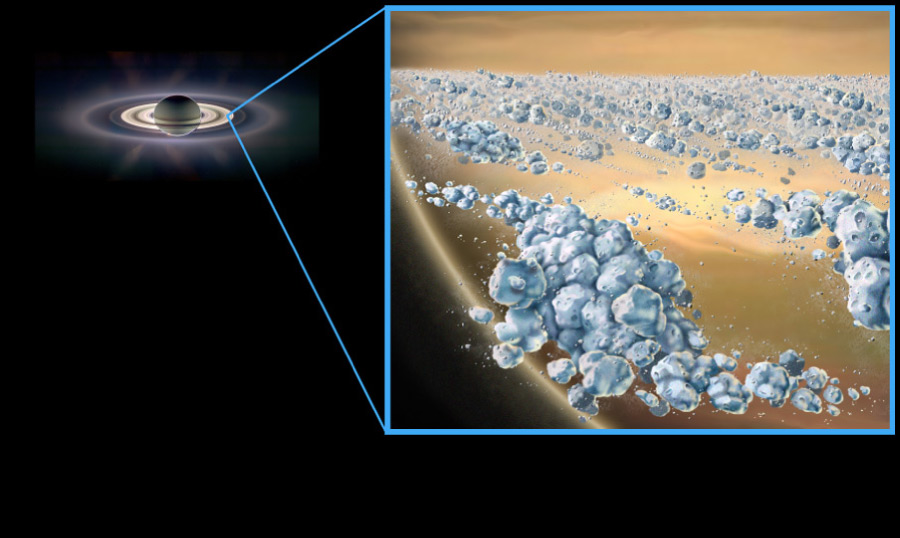
- The rings of Saturn, which are a collection of individual particles orbiting Saturn.
- Disks of material orbiting young stars.
- The disks of spiral galaxies.
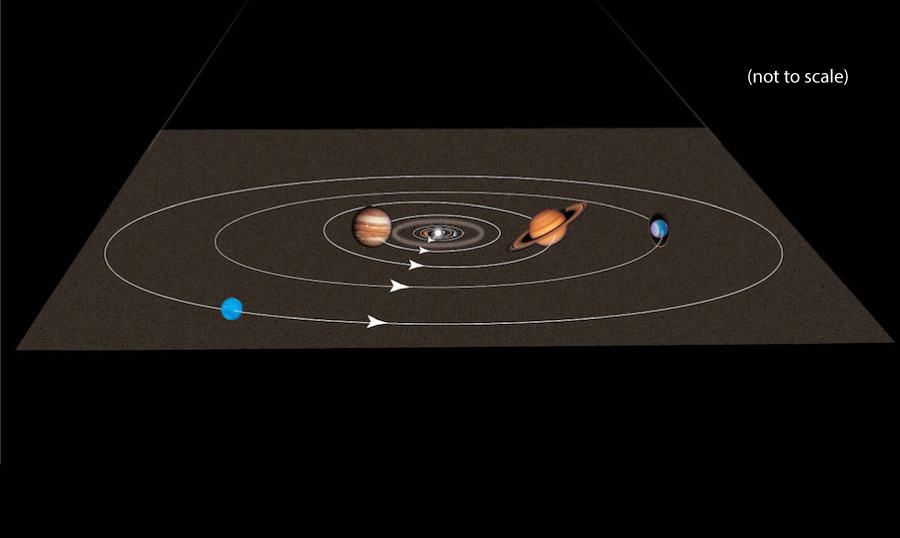
- The orbits of the planets in our solar system, which all trace a fairly flat disk around the Sun.
Why are disks so common? We can again trace the answer to gravity, but this time while also thinking about what happens as gravity collects material together in the first place.
Let’s consider how a star and its planets are born. Observations tell us that stars are born from giant clouds of gas and dust in space. Two things happen at the same time:
- Gravity pulls the material inward, making the cloud shrink in size.
- Like an ice skater pulling in his arms as he spins, the cloud rotates faster and faster as it shrinks (Figure 3.37). (You may recall that this is a result of what we call the “law of conservation of angular momentum.”)
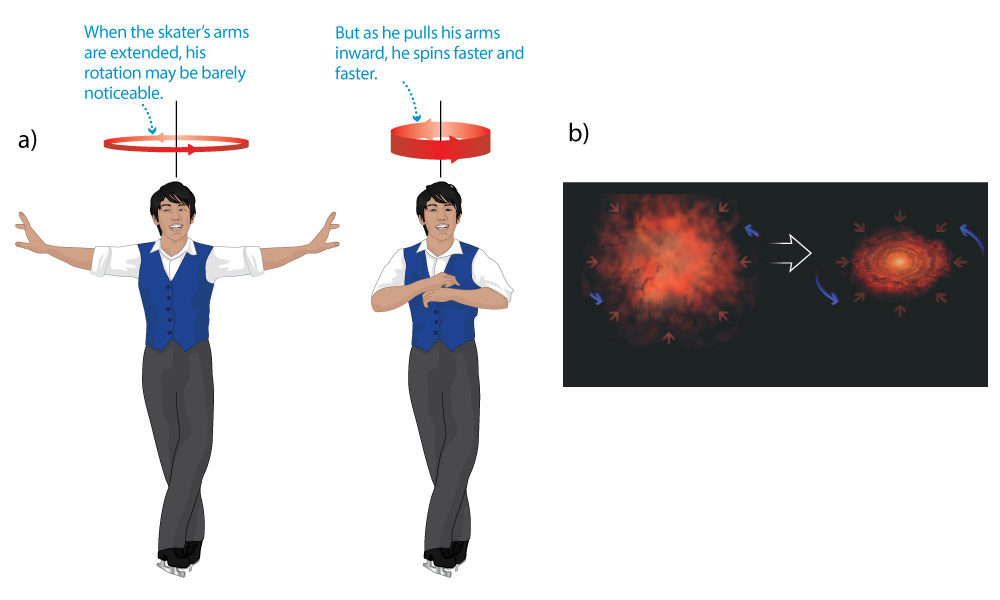
The analogy to the pizza dough below is sufficient for a middle school level of understanding of the flattening process. However, the full reason why the contracting cloud flattens into a disk is a bit more subtle. To understand it, you should think of the cloud of gas and dust as consisting of lots of individual clumps of gas and dust, each orbiting around the center of the cloud. When the cloud first starts to collapse, these clumps may be orbiting with most any random orientation around the center. However, just by random chance, there will be some preferred axis of rotation for the cloud as a whole, determined by the average of all the individual clump orbits around the center. As the cloud collapses, various clumps will begin to collide and merge, and each merged clump will orbit the center with the average velocity of the clumps that formed it. This averaging of their motions will inevitably cause any deviations from the preferred rotation axis to cancel out, so that as the cloud collapses, the clumps will end up all orbiting in approximately the same plane – thereby having formed a disk.
A round star forms at the center of this spinning cloud, where so much material is pulled in by gravity that it essentially become a single object (the star). Meanwhile, the surrounding material flattens into a disk as it orbits around the central star, for much the same reason that spinning a ball of dough will flatten it into a pizza crust (Figure 3.38). Planets (along with moons, asteroids, and comets) can later form from within this disk, which explains why the orbits of planets end up tracing the shape of a disk.
All other disk-like structures in the universe arose for similar reasons: In all cases, gravity drew material together, and the material spun faster and formed a disk as it was drawn inward.

Discussion
Newton’s Epitaph
In addition to discovering the laws of motion and the universal law of gravitation, and inventing calculus, Newton also made many important discoveries about the nature of light and invented the reflecting telescope. Indeed, the compendium of his discoveries is so great that when he died in 1727 (at age 84), the English poet Alexander Pope composed the following epitaph for him:
Nature, and Nature’s laws lay hid in the Night
God said, Let Newton be! and all was Light.
Working in small groups or as a class, consider the following.
- Briefly discuss the meaning of this epitaph, and why it would seem deserved in light of Newton’s many contributions to mathematics and science.
- While Newton made many great discoveries, he also went down some paths that we now know to have been wrong. For example, he spent much of his life doing what was known as “alchemy,” in which he hoped to find chemical processes that could turn other metals into gold — something that we now know is not possible. In addition, on a personal level, Newton often demonstrated behaviors that seem to have been mean or vindictive. (For example, a man named Leibniz apparently invented calculus independently around the same time as Newton, and rather than sharing credit, Newton sought to destroy Leibniz’s career.) Do these facts change your opinion as to whether the epitaph is deserved? Defend your opinion.
The first question simply aims to get students to think about how deeply Newton’s ideas impact our lives even today. The second can generate some interesting philosophical discussion about whether or how much we should let person failings affect our sense of someone’s accomplishments.