Kepler’s Laws
Today we refer to Kepler’s discoveries collectively as Kepler’s laws of planetary motion. He published the work about the first two laws in 1609, and the third law was published in 1619.
Kepler’s 1st Law
We’ve already seen how Kepler’s idea that planets move in ellipses (instead of circles) helped to explain Tycho’s data most accurately. This idea is formalized in Kepler’s first law of planetary motion:
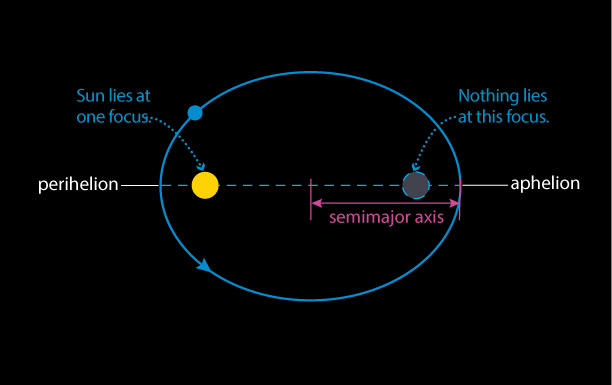
The orbit of a planet is an ellipse with the Sun at one focus.
This law tells us that a planet's distance from the Sun will vary during its orbit. Its closest point is called perihelion (from the Greek for "near the Sun") and its farthest point is called aphelion ("away from the Sun"). The average of a planet's perihelion and aphelion distances is the length of its semimajor axis. Note that while the Sun is located at one focus, there is no physical object at the other focus.
Kepler’s 2nd Law
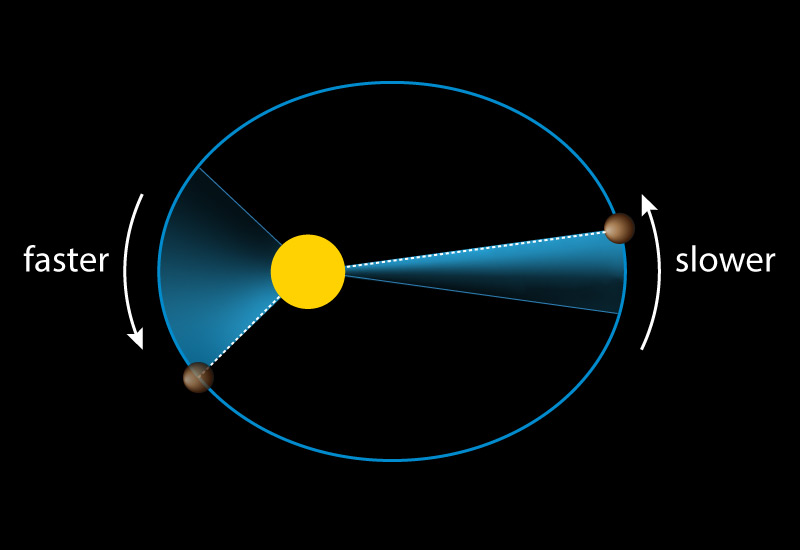
A planet moves faster in the part of its orbit nearer the Sun and slower when farther from the Sun, sweeping out equal areas in equal times.
As shown in the figure to the right, the "sweeping" refers to an imaginary line connecting the planet to the Sun, and as the planet moves the line "sweeps" across an area between the planet and the Sun. Keeping the areas equal means that the planet moves a greater distance (and hence is moving faster) when it is near perihelion than it does in the same amount of time near aphelion.
Kepler’s 3rd Law
More distant planets orbit the Sun at slower average speeds, obeying the precise mathematical relationship p2=a3.
In the mathematical formula, the letter p stands for the planet’s orbital period, which is the time it takes a planet to complete one orbit, measured in years. The letter a represents the planet’s semimajor axis, measured in AU, which is essentially the average distance of the planet from the Sun.
Because Kepler’s third law relates orbital distance to orbital time (period), we can use the law to calculate a planet’s average orbital speed. Doing this shows that planets farther from the Sun orbit at slower average speeds than planets closer to the Sun.