Eccentricity

We know planets move in ellipses, but what exactly is an ellipse?

Ellipses are squashed circles, and a property called eccentricity tells us just how squashed the circle is. Mathematically, eccentricity is defined as the ratio of the distance of each focus from the center of the ellipse, c, to the length of the semi-major axis, a :

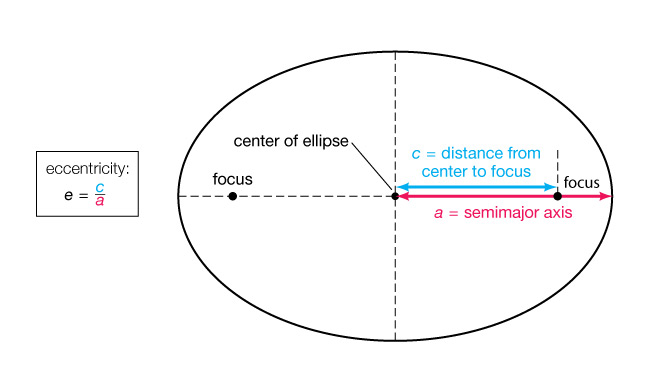
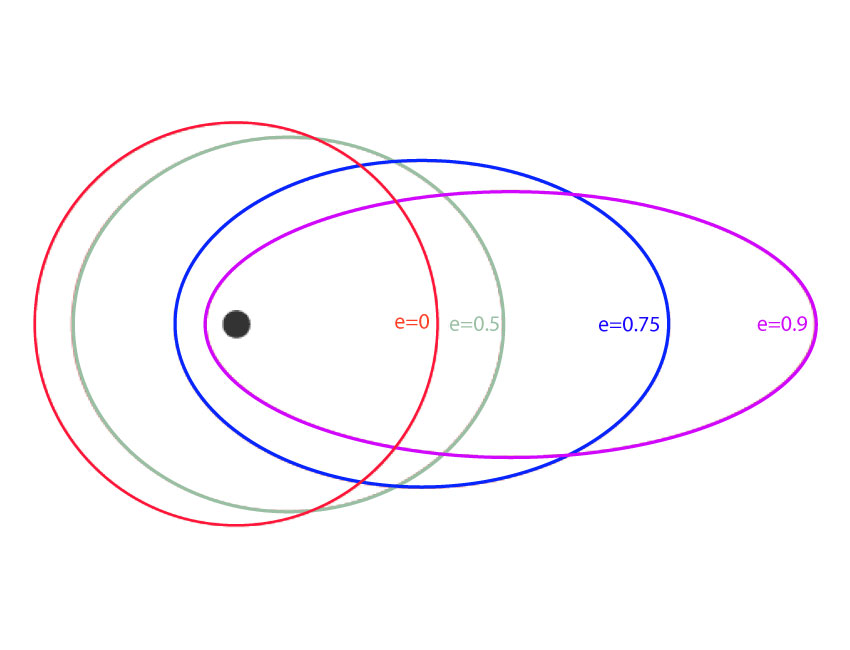
Physically this means that the shape of ellipses varies depending on the eccentricity. Figure 2 shows how ellipses can have an eccentricity of 0 to 0.9, where 0.9 represents the “most squashed” or elongated. Notice how an eccentricity of 0 represents an ellipse with no elongation, or a circle. In other words, a circle is a special case of an ellipse with 0 eccentricity.

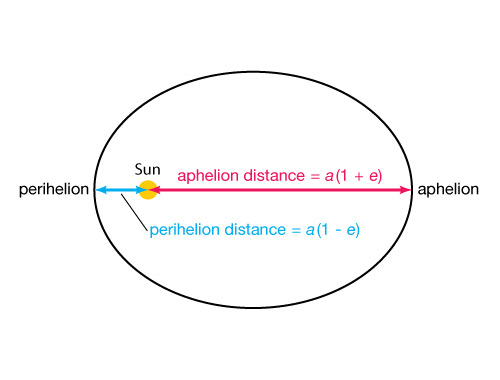
Knowing the eccentricity of an orbit allows us to learn some other interesting physical characteristics about any orbiting body. Perihelion is defined as the point in an orbit where the planet is closest to the sun. Aphelion (pronounced “app-helion”) is the point in its orbit where a planet is farthest from the sun, as shown in Figure 3. Since eccentricity defines the shape of an ellipse about its foci, we can use e to calculate the perihelion and aphelion distances of a planet, using the formulae below:

 
 
 
 

Perihelion distance = a (1-e)

Aphelion distance = a (1+e)

Using the information we just learned, let us answer the questions: At its closest, how far away is Mercury from the Sun? How far away is it at the farthest point in its orbit?

Step 1: Understand the problem

The question is asking you “how far”, which means you are looking for a distance. Specifically, the first question is asking for the shortest distance between Mercury and the Sun. In the discussion above, you learned that this distance is called the perihelion distance, and it can be calculated using the formula:

Perihelion distance = a (1-e)

Similarly, the second question is also asking for a distance (“how far away . . .”), specifically the largest distance between Mercury and the Sun. You know this distance is defined as the aphelion distance, and you can calculate it using the formula:

Aphelion distance = a (1+e)

Step 2: Solve

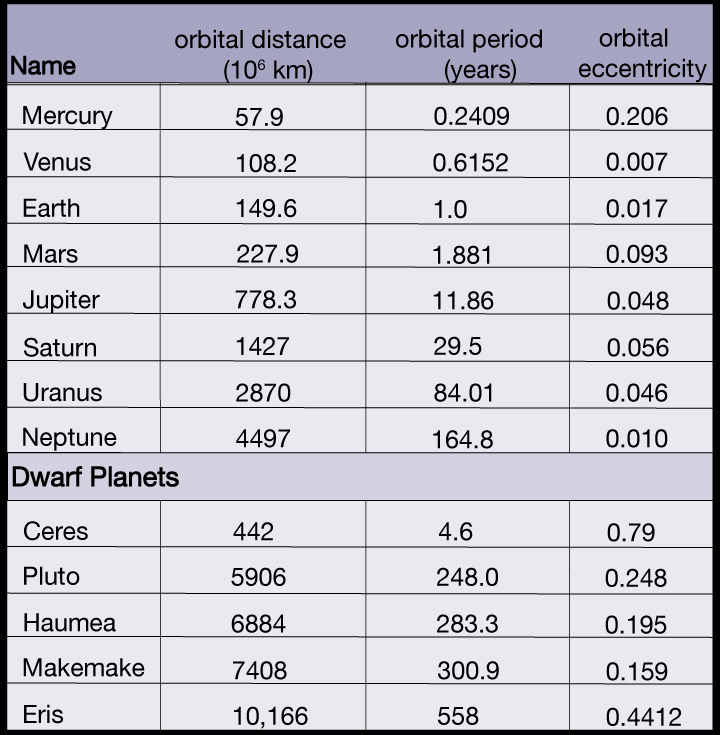
To solve this problem you will need a few values. The eccentricities and semi-major axes of the planets have all been carefully measured and verified, are shown in Table 1. You can use these values to solve your equations for perihelion and aphelion distances.

 
 
 
 

Step 3: Explain

From this calculation we can see that the eccentricity in its orbit means Mercury’s distance from the Sun varies by almost 24 million km, depending on where it is in its orbit. In fact, as you can see from Table 1, Mercury has the most eccentric orbit of all the eight planets in our solar system.

Check your Skills:

Following the example for Mercury, calculate the perihelion and aphelion distances for the Earth.

Check your skills
Following the example for Mercury, calculate the perihelion and aphelion distances for the dwarf planet Eris.