We know that ancient Greek scientists recognized that Earth was round (spherical) by at least 2,500 years ago, because the idea of a round Earth was being taught before about 500 B.C. by the famous Greek mathematician Pythagoras (for whom the Pythagorean theorem is named). No one knows exactly how the Greeks first came to realize that Earth is round (or if other civilizations might have realized the same thing earlier), but at least three key observations clearly contributed to this recognition:
The three key observations are enumerated below. As you read each one, think about the questions that follow each observation; you may wish to discuss the questions with classmates. Then open the answers and make sure you understand how the observation provides evidence that Earth is round.
- Travelers discovered that they saw different constellations as they traveled north or south.
- Based on what you learned in Chapter 2 (especially about how the sky varies with latitude), explain how and why different constellations appear as you travel north or south.
If you look at a model of the celestial sphere (as shown below), you’ll see that with a round Earth at the center, moving north or south changes the set of constellations that you see. For example, as you travel south, you are able to see “new” constellations that cannot be seen from more northern latitudes.
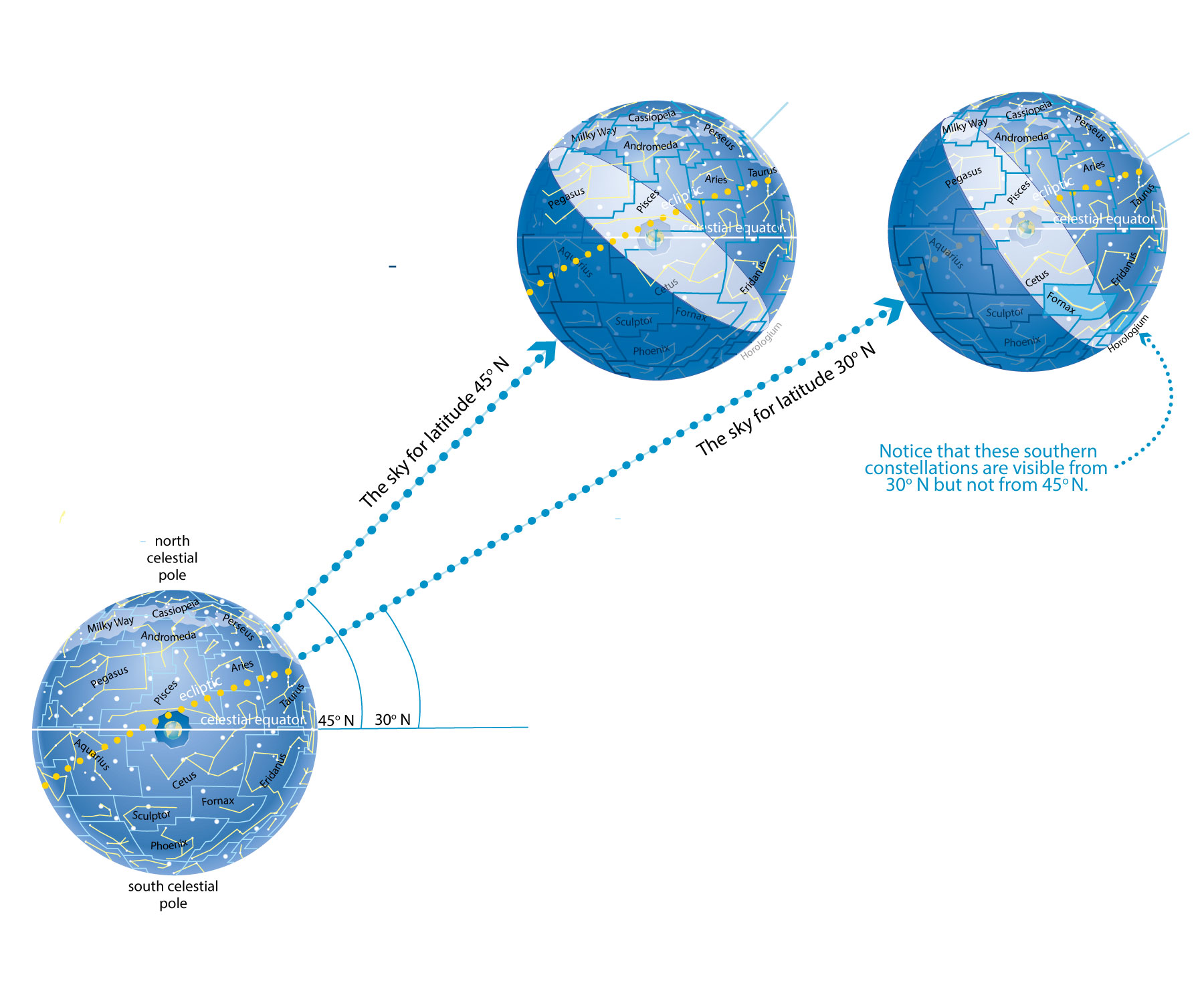
- Does the set of constellations also change when you travel east or west?
No. For any particular latitude, you see the same set of constellations that anyone else at that latitude sees. However, as you know from Chapter 2, different longitudes have particular constellations overhead at different times. Of course, this means that you can notice the east-west change in constellations only if you have an accurate clock with which to compare local time to time at your home, and ancient travelers did not have such clocks and therefore did not recognize the change in constellations with east-west travel.
- Based on your answers to the above two questions, explain why the travelers’ observations proved that Earth must at minimum be curved in a north-south direction (but not necessarily in an east-west direction).
The fact that that the constellations change with north or south travel means Earth must be curved in those directions, because that is the only way to explain how new constellations can come into view (and other constellations drop below the horizon). Note that, without accurate clocks, travel alone could not prove that Earth was also curved east and west. That is why at least one early Greek scientist (Anaximander, c. 610-546 B.C.) guessed that Earth might be cylindrical (like a soda can) in shape, curved only in the north-south direction.
- They noticed that ships sailing into view on the horizon had their masts gradually appear as they approached, and that the horizon became further away when viewed from higher elevations on hilltops or mountains.
When discussing this question, be sure to remind students of the earlier discussion you had in Chapter 2 about “Flaws of the Sky Dome,” since it focuses on the same ideas about the horizon. This will help set the stage for the activity below about debunking flat earth beliefs.
- How did these horizon observations lead to the conclusion that Earth must be curved in all directions (east-west as well as north-south)?
These observations prove that there are parts of the world that are hidden below the horizon no matter which direction you look, which means Earth must be curved in all directions.
- They noticed the curved shadow of Earth on the Moon during lunar eclipses.
- Explain how the curved shadow proves that Earth must be spherical in shape, as opposed to just flat and round like coin.
If you experiment with shadows from a sphere and a coin (as in the Activity “Debunking Flat Earthers” below), you’ll quickly see that the coin gives a round shadow only in a few particular orientations. The fact that the shadow of Earth during eclipses is always curved therefore means that Earth must be spherical, because only a sphere can always cast a round shadow, regardless of orientation.
Together, these three observations leave no doubt that Earth must be round. In fact, not only did the ancient Greeks realize that Earth was round, they even succeeded in measuring its circumference, as discussed in the Do the Math box below.
Today, of course, we have much more direct evidence that Earth is round, because we have observed our planet from space (Figure 3.2).

Group Activity
How Shadow Comparisons Prove Earth is Round
Break up into teams of two or three to demonstrate how the length of shadows depends on the curvature of the Earth. Prepare your materials:
- paper plate
- scissors
- popsicle sticks
- pencil
- bright light bulb or flashlight
Step 1 – Mark two places directly across from each other on the paper plate, near to the edge, but not too close.
Step 2 – Make a small hole on each mark and push a popsicle stick into each hole, so that the popsicle sticks are pointing straight out of the plate (that is, perpendicular to the plate). You can use tape to secure your popsicle sticks to the plate so that they stay pointed straight out.
Step 3 – Have one team member hold the plate vertically in front of the lightbulb or flashlight, while the other team members observe whether there are any shadows cast by the popsicle sticks. Can you find an orientation in which neither popsicle stick casts a shadow? Explore how the shadows of the two popsicle sticks compare when you tilt the plate to different angles relative to the light source.

Step 4 – You can think of the flat plate as representing what Earth would look like if it were flat, and the two popsicle sticks as the locations of two cities on a flat Earth; the light source represents the Sun. Use the observations you have made so far to discuss evidence and reasoning in support of the following:
Claim: “If Earth were flat, then at any particular time, the shadows cast by identical sticks in different cities would all have the same length.”
Step 5 – Bend the paper plate slightly, as though modeling the curvature of the Earth between two cities, then again observe the shadows cast by the popsicle sticks. Do the two sticks still cast shadows of the same length?

Step 6 – Use these additional observations to discuss evidence and reasoning in support of the following claim: “The fact that shadows have different lengths in different cities at the same time proves that Earth cannot be flat.”
This activity is good preparation for the Debunking “Flat Earthers” activity below. It may be useful to have students draw parallels between this paper plate activity and Step 6 in Debunking “Flat Earthers”.
Connections—History
Columbus and the round Earth
A widespread myth gives credit to Christopher Columbus for learning that Earth is round, but knowledge of Earth’s shape predated Columbus by at least about 2,000 years. Indeed, historical evidence indicates that even the general public in Europe knew that Earth was round during Columbus’s time, and that the scholarly debate over whether Columbus’s proposed voyage was doable revolved instead around the question of the distance from Europe to Asia. Using estimates of Earth’s size (going back to measurements like those of Eratosthenes discussed in the Do the Math box above) and of the size of the Eurasian continent, most scholars concluded that the distance from Europe to Asia by sea was too far for the small sailing vessels of the time (that is, they could not carry enough food and supplies). Columbus argued that the distance was actually much shorter. Columbus was the one who was wrong, and his planned voyage to Asia would certainly have ended in disaster if the Americas hadn’t stood in his way. As a side note, some historians suspect that Columbus ultimately received funding for his voyage from the Spanish only because Spanish scholars had heard stories of Viking voyages to the Americas a few hundred years earlier. If true, this implies that the people who sent Columbus on his trip had a better idea of what he would find than Columbus did himself.
Group Activity
Debunking “Flat Earthers”
As we have discussed, humans have known Earth to be round for at least about 2,700 years. Nevertheless, there are some people today (including a few celebrities) who have tried to claim that Earth is flat. Suppose you were to meet someone who makes this claim. How could you prove them wrong? Working in small groups, discuss how each of the following proves that Earth cannot be flat; include diagrams or models whenever possible.
- Horizon distance varies with altitude: If you observe from the top of a tall building, or from a mountain top, you can see farther than you can from lower down. Explain how this proves that Earth cannot be flat.
- Tall ships: If you watch a tall ship sail off, you’ll see its lower parts disappear from view first and its upper parts last. How does this prove that Earth’s surface is curved? Note: if you live near a port where you can actually watch this, it is easiest to notice if you watch the ship through a pair of binoculars or a telescope.
- Clouds: On a day with scattered clouds, all the clouds will be at high altitudes above the ground. But as you look toward the horizon, you will notice that the clouds appear to be lower and lower, and may intersect the horizon in the distance. How does this prove that Earth’s surface is curved?
- Lunar eclipse shadows: Use a light source and objects of various shapes to show that the curvature of Earth’s shadow during lunar eclipses is proof that Earth must be spherical in shape.
- Call a distant friend: Call a friend who lives halfway around the world from you; for example, if you live in the United States, call someone in Australia. You’ll find that if it is daytime for you, it is night time for your friend (or vice versa). Could that happen if Earth were flat?
- Do Eratosthenes’ experiment: Call a friend who lives at least a few hundred kilometers away from you (in any direction), and at the same time, you should each take a ruler of the same length and stand it straight up. Use your cell phones to take pictures and compare the shadows at your two locations, and you will see that one shadow is longer than the other. Explain how this proves that Earth’s surface is curved.
- Fly straight. If you take an airplane flight (or series of flights) always going in the same direction (for example, due east), you’ll eventually end up back where you started.
- Consider the seasons: Recall that seasons are opposite in the northern and southern hemispheres. Would this be possible on a flat Earth?
- Think of as many more proofs as you can to show that Earth is not flat.
- For (1): Students can model this with a “tower” on a flat table top. They will see that relative to a flat table, horizontal lines remain parallel to the surface from different heights on the tower. This means that on a flat Earth, you’d always see the same distance no matter how high you observed from. (Note: for clear air, that distance would be all the way to the “edge” of the flat world; if the air is not perfectly clear, then the distance would be limited by the air clarity, but since you’d be looking through the same amount of air regardless of altitude, you’d still have the same horizon distance at all altitudes.) Alternatively, if you have access to a nearby planetarium or any other structure with curved walls: Have students examine how their view varies depending on how close they stand to the curved wall. If they press a cheek close to the wall, they may only see a short distance along the wall before it has faded below their “horizon” in front of them. But if they take even one step away from the wall, their new vantage point will allow them to see a greater distance along the curved wall, just as we can see a greater distance from a tall tower.
- For (2): If you live near a coast line, try to take your students to do this experiment. Otherwise you can discuss why it occurs by modeling it with a ball and any small object. Have one student be the observer, holding the ball directly in front of her/his own eyes (almost touching their nose), then have another student move an object from the back side of the ball, along the surface towards the observing student, until the observer sees the object. Have them stop exactly when the observing student can first see the object and ask them to describe whether they see all or only part of the object, and which part (top or bottom).
- For (3): On a flat Earth, a horizontal line of sight would always remain the same distance above the ground. Assuming that all the visible clouds are up high, a horizontal line of sight would never intersect with clouds.
- For (4): Most flat Earthers imagine Earth as a round disk, but this cannot produce eclipse shadows, as noted in this tweet from Neil de Grasse Tyson:
- For (5): If Earth were flat, the Sun angle should be the same from all locations, and it would not be possible for it to be daylight in some places and night in others. Note: flat Earthers sometimes try to explain this away by claiming that the Sun shines like a spotlight, but if you make a model using a “spotlight Sun,” you’ll find that it cannot reproduce observed time differences around the world.
- For (6): If you work with another class in another location and do this experiment, you can actually measure the shadow lengths and then calculate Earth’s circumference with the method of Eratosthenes.
- For (7): Circumnavigation could not occur on a flat Earth.
- For (8): Seasons make perfect sense on a round Earth with a tilted axis, but there is no way to reproduce the seasonal pattern with a flat Earth model.
- For (9): There are many more ways to debunk the flat Earth, some easier to demonstrate than others. A few more examples:
- Consider daily motions of stars as discussed in Chapter 2, particularly the fact that stars appear to circle counterclockwise around the north celestial pole as viewed in the northern hemisphere, but clockwise around the south celestial pole in the southern hemisphere.
- Similarly, Earth must be round to explain changes in the Moon’s orientation in the sky with latitude.
- Photos of Earth from space would not always show a round world if Earth were flat; and it would be impossible to see phases of Earth as the Apollo astronauts (and other spacecraft) saw from the Moon.
- Note that even photos from low-Earth orbit — which includes photos from nearly all weather satellites and the ISS — clearly show Earth’s curvature. Since these are used to identify storms and forecast their paths, virtually every weather prediction demonstrates that Earth is round.
- Storm circulation and wind patterns are all shaped by Earth’s rotation (e.g., Coriolis force) – these patterns would make no sense on a flat model.
- The color of sunsets and sunrises is red because we are looking through more atmosphere to see the Sun at those times, which is easy to understand on a round Earth, but makes no sense on a flat model.
- The idea of gravity would not make any sense on a flat world, and what would the world itself be resting upon?
- Note: We highly recommend watching the documentary Behind the Curve (2018), which follows a group of flat Earth believers who essentially end up debunking themselves. You should at minimum watch it for your own edification, and if possible show it to your students (run time 96 minutes) and have some followup discussion.
In today’s world, it is quite likely that your students will have heard flat Earth claims, and some of them may even know someone personally who makes such a claim. As such, it is worth spending some time to show why these claims cannot possibly be correct. A few notes regarding the various suggested activities below:

Group Discussion
Real or Fake?
In small groups or as a class, do a web search on “flat Earth” and briefly explore some of the web sites that you find. How can you tell which ones are presenting legitimate science, and which ones are not? Discuss what lessons the flat Earth claims may contribute to the more general issue of “fake news” in our modern world.
If you’ve done the prior activity on debunking flat Earth claims, you may find it worth also spending a little time with this discussion to connect such claims to the more general issue of how we can distinguish legitimate versus illegitimate claims on the web.