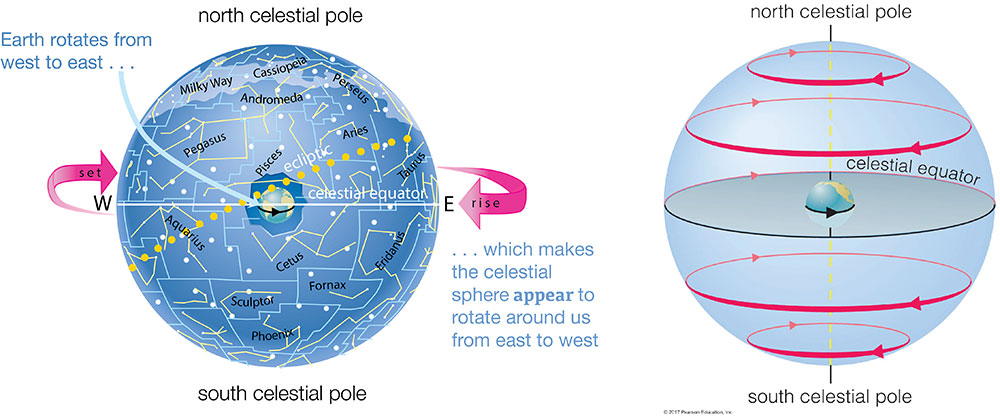
The fact that celestial objects rise in the east and set in the west (or, for circumpolar stars, circle around the north or south celestial pole) each day led the ancient Greeks to assume that the entire celestial sphere rotates around us once each day, going from east to west as shown in Figure 2.9. Of course, today we know that the celestial sphere is just an illusion, and that the reason it appears to rotate around us is because Earth is rotating in the opposite direction — from west to east — once each day. Still, for purposes of understanding what we see in the local sky, it’s useful to use the model of a celestial sphere rotating around us.
As you’ll see, this daily circling of the sky explains all the daily motions we see for celestial objects in the sky, including why some objects just follow daily circles without rising or setting, and why all other objects rise in the east and set in the west.
The Sky at the North Pole
We’ll start with the local sky at the North Pole, which is probably the easiest local sky to understand.
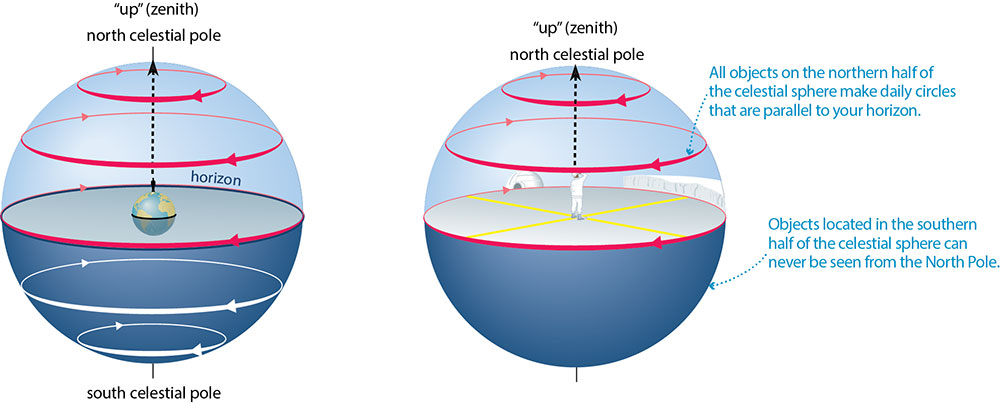
If you add a little stick figure person standing at the North Pole to Figure 2.9, the person would be oriented as shown in Figure 2.10. Imagine that you are standing at that position. Earth itself would be blocking your view of the southern half of the celestial sphere, so your sky would consist only of the northern half, which would be making its daily circles as shown.
Notice that, as viewed from the North Pole, the daily paths of all celestial objects are parallel to the horizon. Therefore, you would see all stars making daily circles around your sky, never rising or setting. In other words, for the sky at the North Pole, all stars are circumpolar. Moreover, your sky would always consist only of the northern half of the celestial sphere, so that you could never see any stars or other objects that are in the southern half of the sphere.
Teacher Notes (Figure 2.10): If your students ask you, here are answers to three common questions that arise with these diagrams and the related discussion; note that these questions are not addressed in the main text because they are beyond the scope of what we expect 8th grade students to learn:
- Q: Isn’t the circle marking the horizon in Figure 2.10 the same one that we called the celestial equator in Figures 2.7 and 2.10? A: Yes; if you were at the North Pole, your horizon would trace out the celestial equator.
- Q: Why isn’t the horizon marked with the directions north, south, east, and west? A: Because if you are at the north pole, all directions are south! This can be a strange concept to students, but you can point out that if you start anywhere on Earth and walk due north, you will eventually reach the North Pole – and if you then continued walking in the same direction, you’d find that you were heading south. Another fun way to address this idea is by asking students to think about the question, “What’s north of the North Pole?” The answer is nothing, since you cannot travel north of the North Pole; in other words, it is in essence a meaningless question.
- Q: Wouldn’t my horizon actually be slightly less than half of the celestial sphere, because Earth “sticks up” a bit in the middle (as shown in part (a))? A: No. Remember that the celestial sphere is only an illusion, made from the way celestial objects all appear to be on a sphere around us — and all these objects are so far away that Earth’s size is insignificant in comparison. That’s why part (b) shows the horizon as an exact match to the celestial equator, with the sky as a full hemisphere (dome).
Group Discussion
The South Polar Sky
In small groups or as a class, discuss:
- How would you change Figure 2.10 to show the sky as it would appear at the South Pole rather than the North Pole?
- Which portion of the celestial sphere would you be able to see from the South Pole?
- Notice that, if you picture yourself at the North Pole as in Figure 2.10, you would see the sky spinning in a counterclockwise direction (around the north celestial pole). Which way would you see the sky spinning at the South Pole? Explain how your answer makes sense given that Earth itself is the only object really spinning, and the entire Earth spins in the same west to east direction.
Teacher Notes: This discussion is optional but should help students prepare for the next subsection in which we begin to consider latitudes that have more complex skies. Key points:
- For (1): The easiest way to answer this is to draw a stick figure person at the South Pole in Figure 2.10a, then turn the diagram upside down so you can see what the sky looks like when your head is pointed up. The sky motion would look very much like the sky motion at the North Pole, with stars tracing daily circles parallel to the horizon.
- For (2): You would see only the southern half of the celestial sphere.
- For (3): From the South Pole, you’d see the sky circling in a clockwise direction. Notice that, as the circular arrows in Figure 2.10 show, the sky is all going the same way, because it is really Earth that is spinning. The change from counterclockwise to clockwise just reflects the fact that you are essentially “upside down” as you look at the sky from the South Pole compared to the North Pole.
Quiz
Note: As always, after you finish the quiz, be sure you read the feedback that explains the correct answers, to make sure you understand the reasons for these answers.
Latitude and Longitude
Before we investigate the local sky elsewhere on Earth, we need to review the coordinates we use to mark locations on Earth, which we call latitude and longitude.
Figure 2.11 shows how these coordinates are defined:
- We use latitude to describe how far north or south of the equator a place is located on Earth, measuring it in degrees (of angle). Latitude is defined to be 0° at the equator, increasing to 90°N at the North Pole and 90°S at the South Pole.
- We use longitude to describe a location’s east-west position. By international treaty, longitude is defined to be 0° along what we call the prime meridian, which passes through Greenwich, England. We then measure longitudes going west or east to the opposite side of Earth, so longitude can go up to 180°W or 180°E, with both of those meaning the same thing.
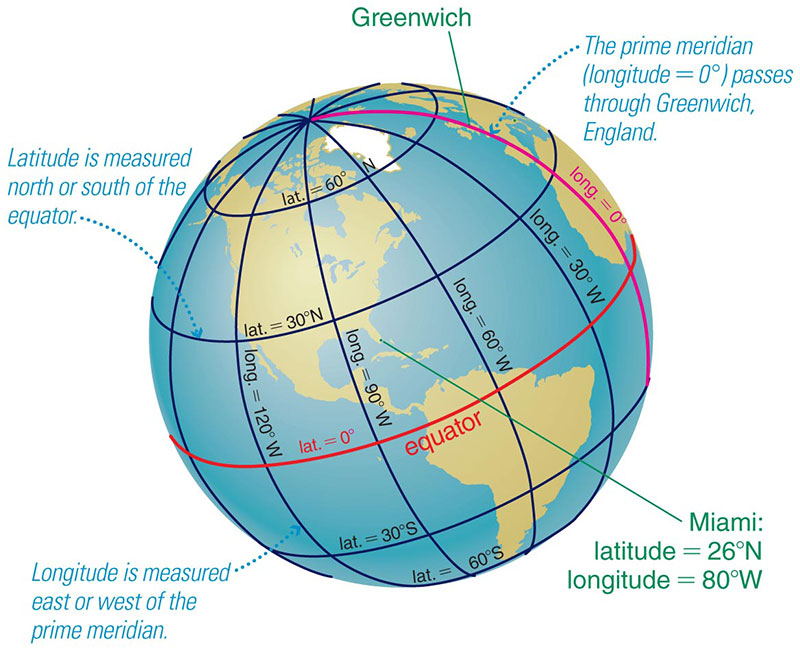
Stating both a latitude and a longitude therefore pinpoints a location on Earth. For example, as Figure 2.11 shows, Miami lies at about 26° N latitude and 80° W longitude.
Activity
Latitude and Longitude
Working individually or in pairs or small groups, use a globe to do the following:
- Find your latitude and longitude.
- Find 3 other cities (or towns) around the world that have the same latitude as you.
- Find 3 other cities (or towns) around the world that have the same longitude as you.
- Imagine that you could somehow drill all the way down to the center of the Earth and then continue until you came out on the other side of the world. What latitude and longitude would that place have? Identify the spot on a globe.
Teacher Notes: This activity should help students understand latitude and longitude through the use of a globe. Note that #4 is much more challenging. An easy but imprecise way for students to do it is to visually identify the “opposite” point on Earth, then read off its latitude and longitude; this will be imprecise because it is difficult to visually identify the exact opposite location. Alternatively, you can get a precise answer with the following procedure:
- For latitude: you can find the latitude of the “opposite” location just by switching north and south. For example, if you are at latitude 40°N, the opposite latitude is 40°S.
- For longitude: the opposite longitude is 180° away from yours, so in principle all you have to do is add 180° to your longitude. But because longitude is only measured up to 180°E or W, this requires a little extra effort. For example, if you are at longitude 105°W, then add the 180° as follows:
- first notice that going westward by 75° from 105°W would get you to 180°W, which is the same as 180°E.
- Since you’ve only gone 75° of the 180° so far, you still need to continue in the same westward direction for another 105°; because you are now starting from 180°E, going westward by 105° takes you to 75°E (because 180–105 = 75).
- You can verify on a globe that 75°E is the longitude directly opposite 105°W.
The Sky at Other Latitudes
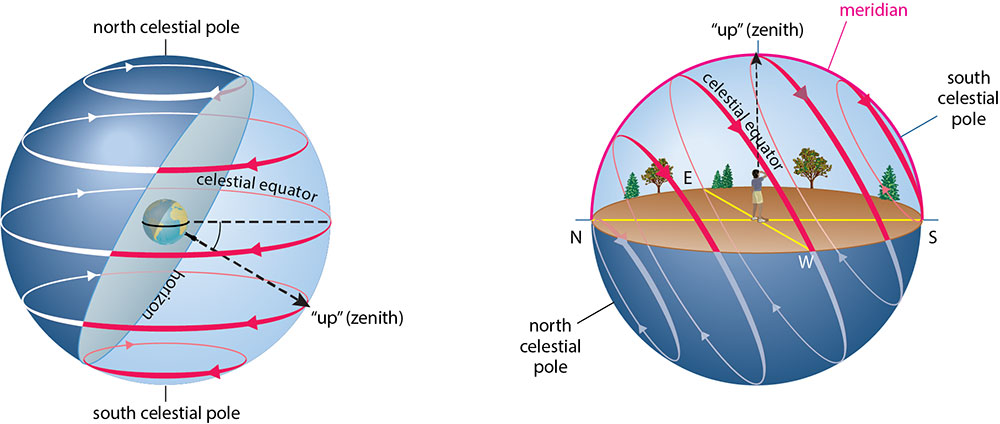
Look again at Figure 2.10, and notice that the horizon at the North Pole cuts the celestial sphere in half. In fact, the horizon must always cut the celestial sphere in half — that is why the local sky always looks like a dome (which is a half-sphere, or hemisphere). The only thing that changes for other latitudes is the angle at which your horizon cuts through the celestial sphere.
Figure 2.12 shows the idea, using a latitude of 40°N (the latitude of cities including Denver, Philadelphia, and Beijing) as an example. Figure 2.12a shows a person standing at latitude 40°N, so you can see where “up” and the horizon are located for that person. If you rotate that diagram so that the person’s “up” is also “up” on your screen, and extend the horizon to look more like a local landscape, then you get the view shown in Figure 2.12b.
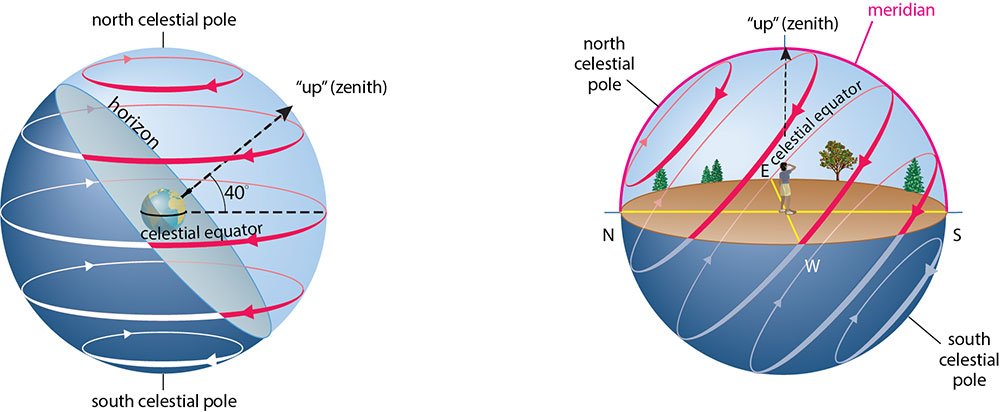
Notice that the celestial sphere is still doing the same thing it always does, which is appearing to turn around us once each day. However, because the horizon cuts through the sphere at an angle, the paths of stars you would see in your local sky at latitude 40° N — or any other latitude — are a little more complex than they were at the North Pole. To help you understand these paths, try to answer each question below, discussing with classmates if you wish. Then click to see the answers.
1. Do any of the circles in Figure 2.12 represent stars that are always above the horizon (circumpolar stars)? If so, which one(s)?
The red circle that is closest to the north celestial pole never falls below the horizon, and the same would be true for any other circumpolar star, meaning any star that makes a daily circle on the celestial sphere that remains above the horizon. In fact, these are the stars that create the circular star trails that we see in photos such as Figure 2.1.
2. For the latitude shown in Figure 2.12, are there any stars on the celestial sphere that would never be seen?
Yes. Any star located far enough south on the celestial sphere so that its daily circle never reaches the horizon (such as the completely white circle in Figure 2.12) would never be seen at this latitude.
3. Which circle(s) in Figure 2.12 represent stars that rise in the east and set in the west each day?
The circles that are partly above the horizon and partly below the horizon. Notice that as stars move around these circles, they appear to rise up on the east side of the sky and then set on the west side.
4. Would it ever be possible that we could discover a star that rises in the west and sets in the east (rather than rising in the east and setting in the west) each day?
No. Remember that the stars are not really circling the Earth; they only appear to be going around us because Earth is rotating. Because Earth rotates from west to east, all stars must appear to rise in the east and set in the west. Note: This rule does not apply to artificial satellites, because they can be orbiting Earth faster than Earth is rotating. You may therefore sometimes see satellites going in almost any direction, including from west to east and north to south.
You can understand the sky at any other latitude in a similar way, following these steps:
Step 1: Start with a diagram like Figure 2.9, showing the way the celestial sphere appears to rotate daily around us.
Step 2: Draw in a horizon that is angled for your latitude, identifying the direction that represents your local “up.”
Step 3: Rotate the diagram so that “up” for your latitude is also up on the screen, so that you can see how celestial objects visible on different parts of the celestial sphere will rise and set, or circle around a celestial pole, in your local sky.
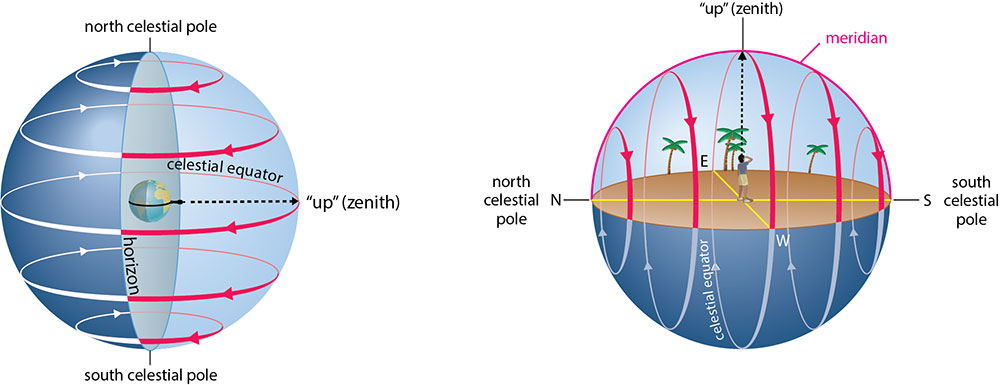
Figure 2.13 shows how this procedure allows us to understand the local sky at the equator (latitude = 0°) and Figure 2.14 does the same for the local sky at latitude 30°S (which cuts through Chile, Argentina, South Africa, and Australia). Study these diagrams and compare them with the ones you already studied for the North Pole (Figure 2.10) and latitude 40°N (Figure 2.12), then you should be ready to answer the quick quiz questions that follow.
Quiz
Note: As always, after you finish the quiz, be sure you read the feedback that explains the correct answers, to make sure you understand the reasons for these answers.
Short Essay Response
Type your answers in the box provided then print the page or take a screenshot and print OR email to your teacher.
Finding Direction by the Stars
If you study the diagrams showing how the local sky at different latitudes cuts through the celestial sphere, and use a little geometry, you’ll notice these interesting facts:
- For anyone living in the Northern Hemisphere: The north celestial pole is located in your local sky due north at an altitude that is equal to your latitude. For example, if you are at the North Pole, which is latitude 90°N, the altitude in your local sky of the north celestial pole is 90° (the zenith). If you are at latitude 40°N, the north celestial pole is located in your local sky due north at altitude 40°.
- For anyone living in the Southern Hemisphere: The south celestial pole is located in your local sky due south at an altitude that is equal to your latitude. For example, if you are at latitude 30°S, the south celestial pole is located in your local sky due south at altitude 30°.
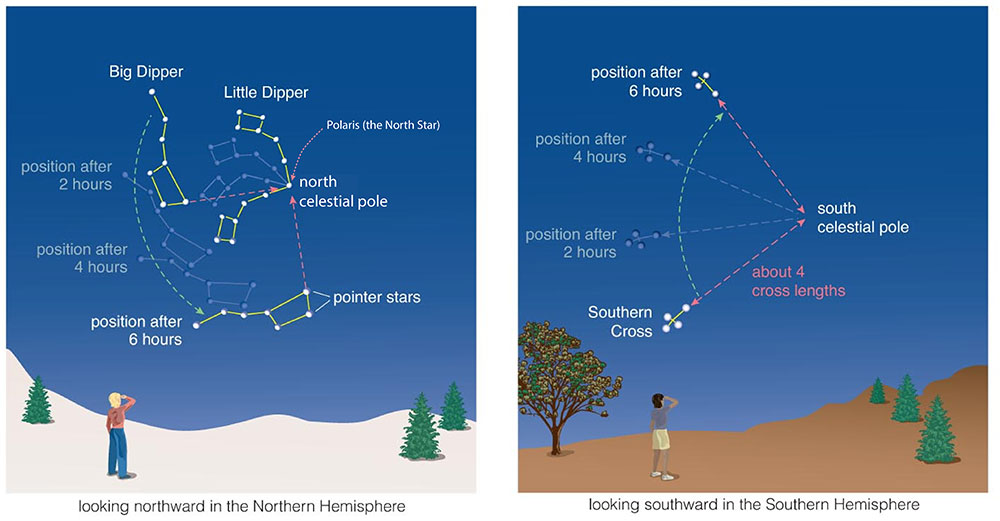
These facts are very useful for navigation, because it means you can determine your latitude simply by finding the north or south celestial pole in your night sky. Figure 2.15 shows how you can use the Big Dipper to help you find the north celestial pole (with the North Star, Polaris, located very close to it) or the Southern Cross to help you find the south celestial pole.
Do the Math
Finding Latitude By the Stars.
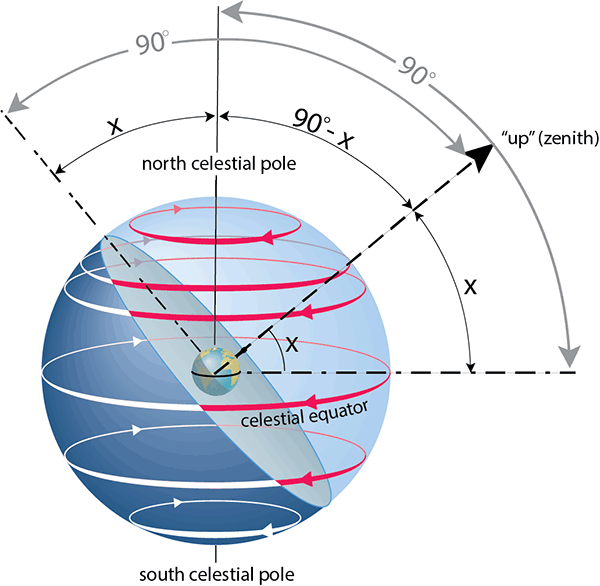
You can probably already see why your latitude must equal the altitude of the north or south celestial pole in your sky, but let’s look at a geometric proof of this fact. The diagram below repeats Figure 2.12a, but to make it more general, we have labeled your latitude as x instead of a specific value. Here are the steps to the proof:
- By definition, your latitude x is the angle that your zenith makes with the extension of Earth’s equator (the celestial equator).
- Also by definition (and as shown), the angle from the celestial equator to the north celestial pole is 90°.
- Therefore, the angle from your zenith to the north celestial pole must be 90° – x, as shown on the diagram.
- By definition (and as shown), the angle from the horizon to your zenith is 90°.
- Therefore, since we’ve already found that the angle from your zenith to the north celestial pole is 90° – x, the angle from your horizon to the north celestial pole must be x, as shown on the diagram.
That is the final result we were looking for: No matter what your latitude x in the Northern Hemisphere, the angle of the north celestial pole above the horizon, which is the altitude of the north celestial pole, must always be equal to x. A similar process shows that the same idea must hold true in the Southern Hemisphere with the south celestial pole.
Quiz
Note: As always, after you finish the quiz, be sure you read the feedback that explains the correct answers, to make sure you understand the reasons for these answers.
Activity
Find Your Celestial Pole.
What is your latitude? Based on your latitude, find the exact location of the north or south celestial pole in your sky.
Teacher Notes: For this activity, students should recognize that the altitude of the celestial pole is equal to your latitude, and that its direction is due north (for the north celestial pole) in the Northern Hemisphere or due south (for the south celestial pole) if you are in the Southern Hemisphere. By now, students should know how to be able to point to the precise altitude and direction of the celestial pole.
Effects of Longitude
Teacher Notes: This is an optional subsection, but it will be useful if you want to give your students a way to refute flat Earth beliefs. In the same way that the fact that we see different sets of constellations at different latitudes proves that Earth is curved in a north-south direction, the fact that we see celestial objects at different times for different longitudes proves east-west curvature. So, together, these facts prove that Earth must be round. In other words: If you want to prove that Earth is round, just call a friend living significantly east or west or you and ask what time it is. The fact that the time differs for people in different places is proof that we live on a round world.
Note that although the sky varies with latitude, it does not vary with longitude, because longitude has no effect on the angle at which your horizon cuts through the celestial sphere. For example, Charleston (South Carolina) and San Diego (California) are at about the same latitude, so people in both cities see the same set of constellations at night.
However, longitude effects the time at which you see particular celestial objects. You can see why by looking again at Figure 2.12. As Earth rotates, making the stars appear to circle around us, different stars will be on the meridian at any given time for different longitudes. For example, when a particular star is directly overhead in Charleston, the same star will still be rising up for people in San Diego, and it won’t reach the horizon until about 3 hours later — by which time it will be on its way downward in the Charleston sky.
The same is true for the Sun, which is why we need different time zones for different longitudes. For example, when it is noon in Charleston (meaning the Sun is near its highest point in the sky), it is about 3 hours earlier (9 a.m.) in San Diego.
Activity
Time Zones.
Look up and answer the following.
- What it the name of the time zone in which you are located? Use a map or globe to find at least two other towns or cities that are in the same time zone.
- What are the names of the time zones to your immediate east and west? Use a map or globe to find at least two towns or cities that are in that time zone.
- Suppose it is noon for you. Use a map or globe to find at least two towns or cities on Earth would be midnight right now. Explain how you know.
- Suppose you can see the Moon in your sky right now. For the two places you identified in (3), would the Moon be in their sky right now? Explain how you know.
Teacher Notes: For students who may not be familiar with time zones, this simple activity can help them learn about them. It is best to do it with a globe so they are focusing on Earth’s roundness, but if you don’t have a globe, it can be done with an online time zone map.
