Put yourself back in the place of someone living in a small village many thousands of years ago. Your sky may look like a dome, but the daily motions of the Sun, Moon, planets, and stars might make you wonder: Where do these objects go when they set below the horizon, and how do they then come rising back up the next day?
Our ancestors surely wondered these same things, though most cultures left few written records of any answers they might have considered. We also know that, by about 2,500 years ago, people in at least some places — notably in ancient Greece — had already recognized that Earth is round rather than flat. This led the ancient Greeks to come up with a new and more sophisticated (compared to the sky dome) model for Earth and sky, one in which they imagined our round Earth to be surrounded by a great celestial sphere (Figure 2.6).
Teacher Notes:
- In this subsection, we state that the ancient Greeks recognized that Earth is round without yet explaining how they drew that conclusion; in case your students ask, just say we’ll be coming back to that, but as you’ll see later, the key reasons appear to have been primarily (1) that they recognized Earth had to be curved in at least a north/south direction because the constellations change with north/south travel; (2) Earth’s curved shadow on the Moon is consistent only with a round Earth.
- For discussion of the celestial sphere: If you have the budget to buy one (typically about $100), it is very helpful to have a model of the celestial sphere so that you can show students the ideas we are discussing. If you decide to buy one, look for one that is clear, so you can see Earth in the middle of it, as in the one shown in Figure 2.6 (right).


Like the sky dome model, today we know that the celestial sphere does not represent reality. For example, as Figure 2.6 shows, the stars we see on the celestial sphere actually all lie at different distances from Earth, and only appear to be part of a single sphere because we lack depth perception when we look into space. However, the celestial sphere is still a useful model, because we can use it to make sense of and predict the motions of celestial objects through our skies.
The first step in making use of the celestial sphere model is to understand what it shows. Notice that the celestial sphere shown on the left in Figure 2.6 is mapped out with all the constellations that appear to surround the Earth. It is also marked with two special points and two special circles:
- If you point straight up from Earth’s north pole, you are pointing at the north celestial pole.
- Similarly, if you point straight away from Earth’s south pole, you are pointing at the south celestial pole.
- If you take Earth’s equator and extend it outward until it meets the celestial sphere, then it becomes the celestial equator.
- If you observe carefully, you’ll recognize that the Sun gradually moves through the constellations over the course of each year, tracing the same circular path from one year to the next. This path is the circle called the ecliptic, which is marked with yellow dots that indicate the Sun’s position among the constellations on different dates throughout the year. Notice that the ecliptic crosses the celestial equator (in two places, one on each side of the sphere) at a 23 1/2° angle.
From our viewpoint on Earth, the Moon and planets also appear to be located on the celestial sphere (that is why, for example, we might say that “Jupiter appears in the constellation of Gemini tonight”). So you might wonder why they are not shown on models of the celestial sphere like that in Figure 2.6. The reason is that, in contrast to the way the Sun follows the same path (the ecliptic) around the celestial sphere year after year, the Moon and planets trace paths that change with time (although they always remain relatively close to the path of the ecliptic). Therefore, there is no simple way to show their paths on the celestial sphere. Indeed, as we’ll discuss later in this chapter in and the next, it was the quest to make sense of the complex paths of the planets that ultimately led to the recognition that Earth is not actually the center of the universe, but instead just one planet going around the Sun.
To make sure that you understand the above ideas, try to answer each question below, discussing with classmates if you wish. Then click to see the answers.
Teacher Notes: You may wish to help students with these questions by making a stick figure person and holding it at different places on a globe, so that students see how different locations on a globe have your head pointing in different directions in space.
1. Where on Earth would you have to be located for the north celestial pole to be at your zenith?
The North Pole. Remember that the zenith is the point directly over your head. If you draw stick figures standing on Earth at various locations, you’ll see that the north pole is the only place where the north celestial pole would be directly overhead.
2. Where on Earth would you have to be located for the south celestial pole to be at your zenith?
The South Pole. In Figure 2.6, people standing at the South Pole would have their heads facing downward, which means the south celestial pole would be directly over their heads (at the zenith).
3. Where on Earth would you have to be located for a point on the celestial equator to be at your zenith?
Anywhere along Earth’s equator. If you draw stick figures on the Earth in Figure 2.6, you’ll see that some point along the celestial equator will be directly overhead for each point on Earth’s equator.
4. Why does the ecliptic cross the celestial equator at an angle of 23½°?
Because that is the tilt of Earth’s axis. Look back at Figure 1.X2, which shows that Earth’s axis is tilted by 23½° relative to its orbit around the Sun. This tilt explains why the Sun appears to trace a path around the celestial sphere that is tilted by the same 23½° to the celestial equator.
Quiz
Note: As always, after you finish the quiz, be sure you read the feedback that explains the correct answers, to make sure you understand the reasons for these answers.
The Milky Way
Teacher Notes: You can consider this subsection on the Milky Way optional, but it does not take long to cover, and most students will be interested to learn how the Milky Way in the sky is related to our Milky Way Galaxy.
Look back at the photo that opens this chapter, in which we see the band of light called the Milky Way stretching up into the sky. This band gets its name from its white, milky appearance. If it is clear enough and dark enough, you can see the Milky Way in your local sky from anywhere on Earth, because this band of light wraps all the way around the celestial sphere (as you can see on the celestial sphere globe at the right in Figure 2.6). You might wonder, what exactly is the Milky Way that we see in the night sky, and why does it share a name with our Milky Way galaxy?
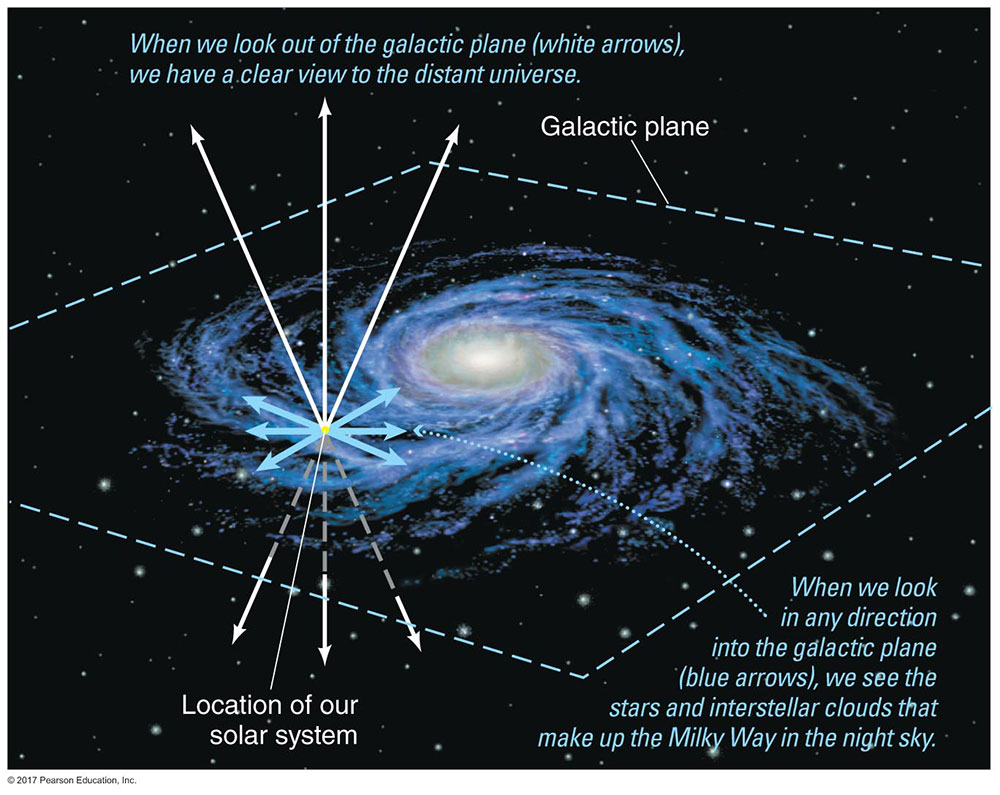
To understand the answer, recall from Chapter 1 that our galaxy has a fairly flat disk, much like a pancake, and that we live inside it, at a location like that indicated in Figure 2.7. Because the disk is so thin, and stars are so widely spaced out, we have a clear view “out of the pancake” to the distant universe in most directions we can look. However, when we try to look in any direction that is “into the pancake,” we are looking into the disk of our galaxy. The disk contains so many stars — plus interstellar clouds of gas and dust — that everything blends together into a milky white band of light. This band makes the circular ring of the Milky Way going all the way around the celestial sphere.
Teacher Notes: It can be fun to actually talk about the pancake analogy to the galaxy as follows: Imagine that you lived inside a pancake, and you envision your “sky” as a sphere centered on your location. As long as the pancake were thin enough, it would be mostly transparent in most directions; in the analogy, this means that in most directions, you’d see only the relatively few stars between you and the outside of the disk. But when you look in any direction within the pancake, whether toward the center or toward any of the edges, all you would see is lots of pancake dough. In other words, your “sky” would be fairly clear in most directions, but you’d see a circular ring of dough going all the way around your sky, just as we see the Milky Way going all the way around the celestial sphere.
- Note: Our galaxy’s diameter is actually about 100 times its thickness, which means it’s more like a crepe than a pancake. However, the distance that we see into the galaxy (that is, the distances to the stars we can see by naked eye on the celestial sphere) is very small compared to the galaxy’s size, which is why the Milky Way appears as a fairly wide band in our sky.
Connections—Etymology
Galaxies
Figure 2.7 shows why the band of light we call the Milky Way in our sky shares a name with our Milky Way Galaxy, but the semantic connection actually goes deeper: The word galaxy comes from the Greek galactos, which means “milk.” In that sense, the very term galaxy traces back to the milky appearance of the band of light we call the Milky Way in our sky.
Connections—History
Learning about Galaxies
To our naked eyes, the Milky Way in our sky doesn’t really look like a bunch of stars; it just looks milky. In fact, we didn’t learn that the Milky Way is made up of countless individual stars until Galileo pointed his telescope at it in 1610. Later, as people built better telescopes, they began to discover the spiral-shaped structures in the sky that we now know to be other galaxies. However, until about a century ago, telescopes were not yet powerful enough to show whether the spirals were distant collections of stars or much nearer gas clouds, and as a result, scientists debated this issue for almost two hundred years. Finally, in 1924, Edwin Hubble used what was then the world’s largest telescope to prove that the Andromeda spiral was in fact a collection of individual stars. After that, there was no longer any doubt that our Milky Way Galaxy is just one among billions of galaxies in the universe.
Angular Sizes and Distances
Teacher Notes: This subsection is also optional, but students may find it useful to be able to estimate angles on the sky with their outstretched hand, as shown in the figure. Note that the angles shown in the figure work for almost everyone, regardless of size. The reason is that people with smaller hands also tend to have shorter arms, so it is still true that, for example, a single finger (on your outstretched arm) will subtend approximately a 1° angle on the sky.
Our lack of depth perception on the celestial sphere makes it difficult to judge the true sizes or separations of the objects we see in the sky. However, by measuring angles across things or between things, we can only describe what we call angular sizes or separations.
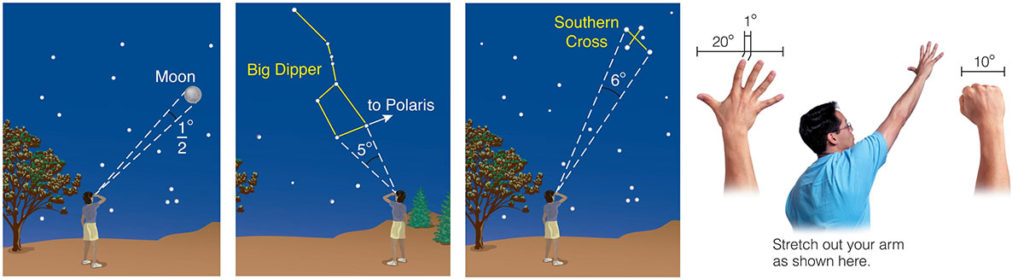
Figure 2.8 shows the idea:
- For objects like the Moon, we can measure the angle across it in the sky. For the Moon, this angle turns out to be about ½°, so we say the Moon has an angular diameter of about ½°.
- We can similarly measure the angles that separate two stars in the sky, such as the two “pointer stars” of the Big Dipper or the stars that mark two ends of the Southern Cross
- You can use your outstretched arm as an approximate angle measuring device. For example, a single finger covers an angle of about 1° in the sky, while your closed fist spans an angle of about 10°.
Activity
Angle Estimation
Use your outstretched hand to estimate several angles in the sky. For example, find the current altitude of the Sun, or the angular distance between two distant buildings as viewed from your location.
It’s important to remember that angular sizes and distances do not by themselves tell us about true sizes or distances. For example, the Sun and Moon have about the same angular size, but the Sun is actually about 400 times as large in diameter as the Moon; the reason it has the same angular diameter as the Moon is because it is also about 400 times as far away.
Group Discussion
It was THIS Big!
Young children often try to describe the sizes of objects in the sky (such as the Moon or an airplane) in units like inches or miles, or by holding their fingers apart and saying “it was THIS big.” Can we really describe objects in the sky in this way? In small groups or as a class, briefly discuss why or why not.
Teacher Notes: This is a very brief discussion topic, designed to get students to think about the difference between physical sizes and angular sizes, and why we can’t use physical dimensions when describing angles in the sky:
Quiz
Note: As always, after you finish the quiz, be sure you read the feedback that explains the correct answers, to make sure you understand the reasons for these answers.